18 基礎概念

学習目標

ケンドールの記号を理解する．
利用率を理解し，計算できる．
滞在時間，待ち時間，系内客数，待ち行列長などの評価指標を理解する．
リトルの法則を理解し，適用できる．
\(G/G/1\)，\(G/G/c\) 待ち行列の基本的な関係式を理解する．

18.1 待ち行列とは

客（customer）がシステムに到着（arrival）し，待ち行列（queue）に並び，サービスを受け，最後にシステムを退出（departure）する．図 18.1 は，典型的な待ち行列システムを示している．

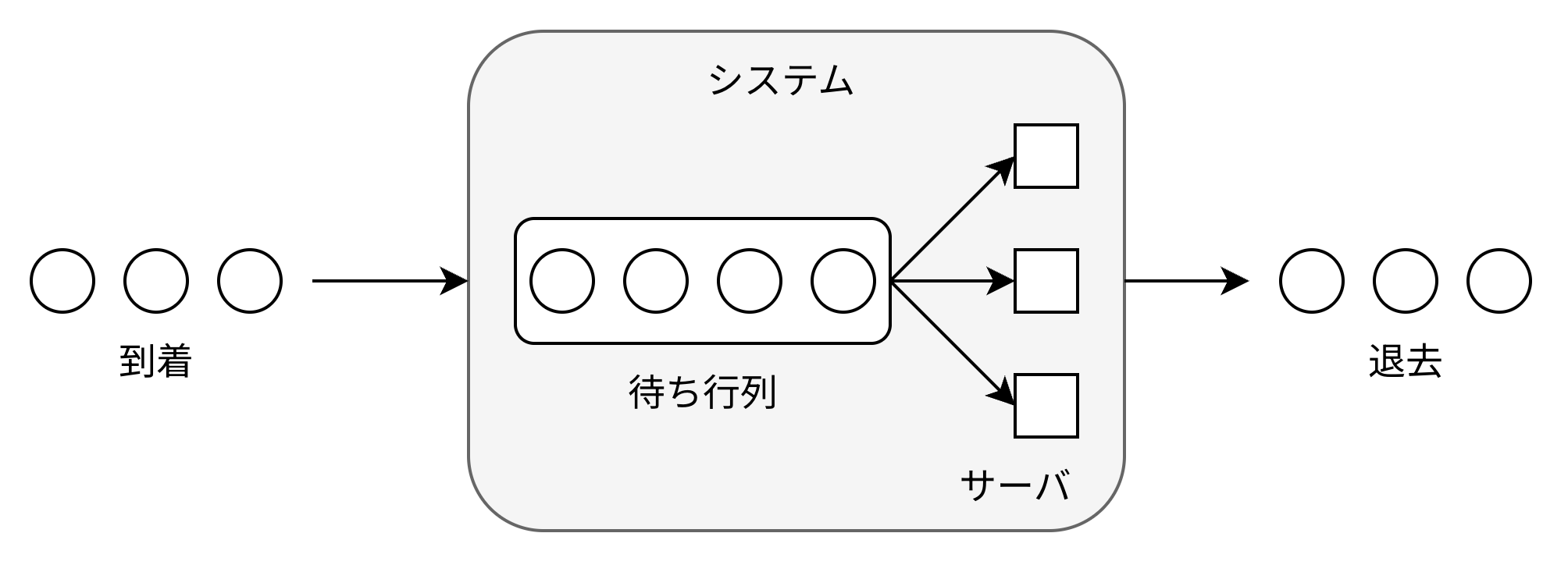
待ち行列システムは待ち行列とサーバから構成される．これ以降は，待ち行列システムを単にシステムと呼ぶことにする．

18.2 待ち行列モデル

一般に，待ち行列モデルは，次の5つの要素で特徴付けられる．

客の到着過程
サービス時間分布
サーバ数
システム容量
サービス規律

18.3 ケンドールの記号

待ち行列モデルは，ケンドールの記号（Kendall’s notation）により表現する．通常以下の形式で表される．

\[ A/B/X \]

ここで，\(A\) は到着間隔分布の種類，\(B\) はサービス時間分布の種類，\(X\) はサーバ数を表す．また，システム容量は無限大であり，サービス規律は FCFS であると仮定する．

\(A\) と \(B\) には以下の記号が用いられる．

記号	意味
\(M\)	指数分布
\(D\)	決定論的
\(G\)	一般分布
\(E_k\)	\(k\) 次アーラン分布
\(H_k\)	\(k\) 次超指数分布

例えば，客の到着間隔が指数分布に従い，サービス時間が一定であり，サーバ数が1台である待ち行列モデルは，\(M/D/1\) 待ち行列と表される．この \(M/D/1\) 待ち行列モデルのシステム容量は無限大であり，サービス規律は FCFS であると仮定されている．

\(G/G/1\) と \(G/G/c\) 待ち行列は，特定の分布を仮定しない待ち行列モデルであるため，得られた結果は多くの待ち行列モデルに適用できる．さらに，\(G/G/c\) 待ち行列から得られた結果は，\(c = 1\) とすると，\(G/G/1\) 待ち行列に適用できる．

なぜ指数分布は \(M\) と書くのか

アーラン分布 \(E_k\) と間違えないようにするため．
指数分布のマルコフ性（Markovian property）と無記憶性（memoryless property）に由来する．

18.4 利用率

\(G/G/c\) 待ち行列モデルを考える．記号のまとめを以下に示す．

記号	意味
\(\lambda\)	平均到着率，単位時間あたりの到着客数の平均
\(L\)	系内客数
\(W\)	滞在時間
\(L_q\)	待ち行列長
\(W_q\)	待ち時間
\(S\)	サービス時間
\(\mu\)	平均サービス率，単位時間あたりに処理できる客数の平均
\(c\)	サーバ数
\(\rho\)	利用率

時刻 \(t\) までに累積到着客数を \(A(t)\) とする．時間区間 \([0,t]\) における単位時間あたりの到着客数の平均は \[ \bar{A}(t) = \frac{A(t)}{t} \] で与えられる．以下の極限 \[ \lambda = \lim_{t \to \infty} \bar{A}(t) \] が存在するとき，\(\lambda\) を平均到着率（average arrival rate）と呼ぶ．平均到着率 \(\lambda\) は，長期的に見たときの単位時間あたりの平均到着客数を表す．

\(S\) をサービス時間を表す確率変数とする．平均サービス時間 は \(\mathbb{E}[S]\) で表される．単位時間あたりに一つのサーバが処理できる平均客数は \[ \mu = \frac{1}{\mathbb{E}[S]} \] で計算する．\(\mu\) を平均サービス率（average service rate）と呼ぶ．

例 18.1 あるゼミでは，学生6人と教員1人が所属している．教員は，1人の学生に対して平均して10分間指導を行う．このとき，平均サービス率と平均サービス時間を求めよ．

平均サービス時間 \(\mathbb{E}[S]\) は10分である．平均サービス率 \(\mu\) は次のように計算される．

\[ \mu = \frac{1}{\mathbb{E}[S]} = \frac{1}{10 \text{ 分}} = \frac{1}{10/60 \text{ 時間}} = 6 \text{ 人/時間} \] すなわち，教員は1時間あたり平均6人の学生に指導を行うことができる．

システムの利用率 \(\rho\) は，次の式で定義される．

\[ \rho = \frac{\lambda}{c \mu} \]

ここで，\(c\) はサーバ数を表す．利用率 \(\rho\) は，到着率 \(\lambda\) がシステムの処理能力 \(c \mu\) に対してどの程度であるかを示す指標であり，システムの忙しさを表す．\(G/G/1\) 待ち行列の場合，\(c = 1\) であり，利用率は \(\rho = \lambda / \mu\) となる．

\(\rho > 1\) の場合，\(\lambda > c \mu\) となり，待ち行列が無限に増加する．\(\rho = 1\) の場合，\(\lambda = c \mu\) となり，到着率とシステムのサービス能力が等しい．\(D/D/1\) 待ち行列のように，客の到着間隔とサービス時間がともに一定である場合を除き，待ち行列は無限に増加する．したがって，システムが安定して運用されるためには，\(\rho < 1\) である必要がある．

\(\lambda\) と \(\mu\) が与えられたとき，\(\rho < 1\) という条件を用いて，システムが必要なサーバ数 \(c\) の最小値を求めることができる．すなわち，

\[ \rho = \frac{\lambda}{c \mu} < 1 \]

を満たす最小の整数 \(c\) を求めればよい．

例 18.2 あるコールセンターでは，オペレーター10人が勤務している．1件の電話対応に平均して10分かかる．1時間あたり30件の電話がかかってくるとする．

社員一人1時間あたりに対応できる電話の平均件数を求めよ．
このコールセンターの利用率を求めよ．
待ち行列が無限に増加しないために必要な最小のオペレーター数を求めよ．

平均サービス時間 \(\mathbb{E}[S] = 10 \text{ 分} = 1/6 \text{ 時間}\) である．平均サービス率 \(\mu\) は \[ \mu = \frac{1}{\mathbb{E}[S]} = \frac{1}{1/6} = 6 \text{ 件/時間} \] となる．すなわち，社員一人は1時間あたり平均6件の電話に対応できることになる．

平均到着率 \(\lambda\) は30件/時間，平均サービス率 \(\mu\) は6件/時間，サーバ数 \(c\) は10である．利用率 \(\rho\) は次のように計算される．

\[ \rho = \frac{30}{10 \times 6} = \frac{30}{60} = 0.5 \]

よって，このコールセンターの利用率は0.5である．

安定した運用のためには，\(\rho < 1\) を満たす必要がある．すなわち，

\[ c > \frac{\lambda}{\mu} = 5 \]

したがって，最小でオーペレーター6人が必要である．

18.5 定常状態

システムの使用を開始してから十分時間が経過していなく，システムの状態（システムにいる客数など）が初期状態の影響を受けている場合，システムは過渡状態（transient state）にあるという．一方で，システムの使用を開始してから，十分時間が経過した後，システムの状態は初期状態の影響を受けなくなる．このとき，システムは定常状態（steady state）にあるという．

過渡状態よりも定常状態の方が，解析が容易であるため，ここで紹介する待ち行列理論では定常状態におけるシステムの性能評価が主に扱われる．以下では，定常状態における記号を紹介する．

システム内にいる客数のことを系内客数と呼ぶ． \(N(t)\) を時刻 \(t\) における系内客数とする．\(\mathbb{P}(N(t) = n)\) を時刻 \(t\) における系内客数が \(n\) である確率とする．\(L\) を定常状態における系内客数とすると，\(\rho < 1\) のとき，\(n = 0, 1, 2, \ldots\) に対して，

\[ \pi_n = \mathbb{P}(L = n) = \lim_{t \to \infty} \mathbb{P}(N(t) = n) \]

が存在し，\(\pi_n\) は系内客数 \(L\) が \(n\) である確率を表す．もう一つの解釈として，\(\pi_n\) は系内客数が \(n\) である時間の割合を表すとも言える．\(\pi_n\) は時刻 \(t\) に依存しない．

滞在時間は客がシステムに到着してサービスを受け，システムを退出するまでにかかる時間である． \(W^{(k)}\) を客 \(k\) の滞在時間とする．\(W\) を定常状態における滞在時間とすると， \(\rho < 1\) のとき，

\[ F_W(t) = \lim_{k \to \infty} \mathbb{P}(W^{(k)} \leq t) \]

が存在し，\(F_W(t)\) は滞在時間 \(W\) が \(t\) 以下である確率を表す．

18.6 リトルの法則

以上では，定常状態における系内客数と滞在時間の分布を紹介した．待ち行列システムの性能を評価するた際に，もっとも興味がある指標には，平均系内客数，平均滞在時間などがある．

以下の極限が存在するならば，平均系内客数 \(\mathbb{E}[L]\) と平均滞在時間 \(\mathbb{E}[W]\) はそれぞれ次の式で定義される． \[ \mathbb{E}[L] = \lim_{T \to \infty} \frac{1}{T} \int_0^T N(t) dt \]

\[ \mathbb{E}[W] = \lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^n W^{(k)} \]

すなわち，平均系内客数は，長期的に見たときのシステム内の平均客数を表し，平均滞在時間は，長期的に見たときの客の平均滞在時間を表す．

リトルの法則（Little’s Law）は，待ち行列理論における基本的な関係式であり，平均系内客数 \(\mathbb{E}[L]\)，平均滞在時間 \(\mathbb{E}[W]\)，平均到着率 \(\lambda\)の関係を示すものである．リトルの法則は

\[ \mathbb{E}[L] = \lambda \mathbb{E}[W] \]

と表される．すなわち，平均系内客数 \(\mathbb{E}[L]\) は，平均到着率 \(\lambda\) と平均滞在時間 \(\mathbb{E}[W]\) の積に等しい．

Little (1961) と Stidham (1974) により，リトルの法則の厳密な証明が与えられている．ここでは，例を用いて，リトルの法則を直感的に理解する．

例 18.3 (大学の在籍学生数) ある大学の経営システム系では，毎年80人の新入生が入学し，卒業までに4年間在籍する．このとき，経営システム系に在籍している学生の平均人数を求めよ．

平均到着率 \(\lambda\) は80人/年，平均滞在時間 \(\mathbb{E}[W]\) は4年である．リトルの法則により，平均系内客数 \(\mathbb{E}[L]\) は次のように求められる．

\[ \mathbb{E}[L] = \lambda \mathbb{E}[W] = 80 \times 4 = 320 \text{ 人} \]

よって，経営システム系には320人の学生が在籍していることになる．

例 18.4 (銀行の平均在店客数) ある銀行では，1時間に平均20人の客が来店し，各客が銀行に滞在する平均時間は12分である．このとき，この銀行には平均何人の客がいるか．

平均到着率 \(\lambda\) は20人/時間，平均滞在時間 \(\mathbb{E}[W] = 12 \text{ 分} = 12/60 \text{ 時間}\) である．リトルの法則から，平均系内客数 \(\mathbb{E}[L]\) は

\[ \mathbb{E}[L] = \lambda \mathbb{E}[W] = 20 \times \frac{12}{60} = 4 \text{ 人} \]

となる．すなわち，銀行内には平均して4人の客が滞在する．平均滞在時間 \(\mathbb{E}[W]\) や平均到着率 \(\lambda\) が増加すると，平均系内客数 \(\mathbb{E}[L]\) も増加することがわかる．

これまでは，システム全体に関するリトルの法則を紹介したが，待ち行列を「システム」として考えた場合にも同様の関係が成り立つ．すなわち，リトルの法則を待ち行列にも適用できる．待ち行列に関するリトルの法則を説明するために，待ち時間と待ち行列長の記号を導入する．

待ち時間は，客がシステムに到着してからサービスを受けるまでの時間であり，滞在時間は待ち時間とサービス時間の和に等しい．待ち行列長は，システム内にいる客数のうち，サービスを受けていない客数を表す．待ち行列長を \(\mathbb{E}[L_q]\)，平均待ち時間を \(\mathbb{E}[W_q]\)，平均到着率を \(\lambda\) とすると，

\[ \mathbb{E}[L_q] = \lambda \mathbb{E}[W_q] \]

が成り立つ．

18.7 \(G/G/1\)，\(G/G/c\)

\(G/G/1\) と \(G/G/c\) 待ち行列において，\(\mathbb{E}[L]\)，\(\mathbb{E}[W]\)，\(\mathbb{E}[L_q]\)，\(\mathbb{E}[W_q]\) の関係式を紹介する．

客がシステムに到着してから退出するまでの平均滞在時間 \(\mathbb{E}[W]\) は，平均待ち時間 \(\mathbb{E}[W_q]\) と平均サービス時間 \(\mathbb{E}[S]\) の和で表される．すなわち，

\[ \mathbb{E}[W] = \mathbb{E}[W_q] + \mathbb{E}[S] = \mathbb{E}[W_q] + \frac{1}{\mu} \]

である．リトルの法則により，

\[ \mathbb{E}[L] = \lambda \mathbb{E}[W] = \lambda \left( \mathbb{E}[W_q] + \frac{1}{\mu} \right) =\lambda \mathbb{E}[W_q] + \frac{\lambda}{\mu} = \mathbb{E}[L_q] + \frac{\lambda}{\mu} \]

が成り立つ．\(\mathbb{E}[L] = \mathbb{E}[L_q] + \lambda /\mu\) が成立するから，\(\lambda / \mu\) はサービスを受けている客数の平均を表していると言える．また，\(\lambda / \mu\) は稼働中のサーバ数の平均を表しているとも言える．

\(\mathbb{E}[L]\)，\(\mathbb{E}[W]\)，\(\mathbb{E}[L_q]\)，\(\mathbb{E}[W_q]\) は待ち行列における基本的な評価指標である．\(\lambda\) と \(\mu\) が与えられたとき，4つの指標のうち1つがわかれば，残りの3つを計算できる．

18.8 用語集

英語	日本語
service facility	サービス施設
server	サーバ
number of servers	サーバ数
interarrival time	到着間隔
service time	サービス時間
arrival rate	到着率
service rate	サービス率
offered load

18.9 演習問題

練習 18.1 (アイスクリーム屋さん) あるアイスクリーム屋さんでは，1名の店員が客の注文を受け付け，アイスクリームを提供している．平均して，1時間に30人の客が来店している．店員は，1時間に60人の客に対応できる．客の平均待ち時間を \(5\) 分とする．

このアイスクリーム屋さんの利用率を求めよ．
客の平均滞在時間，平均系内客数，平均待ち行列長を求めよ．

解答 18.1. 平均到着率 \(\lambda\) は30人/時間，平均サービス率 \(\mu\) は60人/時間である．サーバ数 \(c = 1\) であるため，利用率は

\[ \rho = \frac{30}{1 \times 60} = 0.5 \] となる．

平均サービス時間 \(\mathbb{E}[S] = 1 \text{ 分}\)，平均待ち時間 \(\mathbb{E}[W_q] = 5 \text{ 分}\) であるから，平均滞在時間 \(\mathbb{E}[W]\) は

\[ \mathbb{E}[W] = \mathbb{E}[W_q] + \mathbb{E}[S] = 5 + 1 = 6 \text{ 分} \] となる．リトルの法則により，平均系内客数 \(\mathbb{E}[L]\) は \[ \mathbb{E}[L] = \lambda \mathbb{E}[W] = 30 \times \frac{6}{60} = 3 \text{ 人} \] となる．同様に，平均待ち行列長 \(\mathbb{E}[L_q]\) は \[ \mathbb{E}[L_q] = \lambda \mathbb{E}[W_q] = 30 \times \frac{5}{60} = 2.5 \text{ 人} \] となる．