22  出生死滅過程

22.1 学習目標

  • 出生死滅過程の定義と，遷移確率図の読み方を理解する．
  • 大域平衡方程式と局所平衡方程式を導出できる．
  • 定常状態確率 \pi_n を求めることができる．
  • \pi_n から平均系内客数などの評価指標を求めることができる．
  • M/M/1 モデルの定常状態確率と評価指標を導出できる．

22.2 出生死滅過程とは

出生死滅過程では，時刻 t における生物集団の個体数を X_t で表す．これを状態（state）とも呼ぶ．状態 X_t は状態空間 \{0, 1, 2, \ldots\} 上に値をとる．状態遷移（state transition）は，個体の出生または死滅によって引き起こされる．出生死滅過程では，状態遷移は隣接する状態間でのみ発生する．状態 n から状態 n+1 に遷移する確率を \lambda_n，状態 n \geq 1 から状態 n-1 に遷移する確率を \mu_n と表す．すなわち，

\lambda_n = P(X_{t+1} = n+1 | X_t = n), \mu_n = P(X_{t+1} = n-1 | X_t = n).

出生死滅過程の遷移確率図は以下に示す．

BirthDeathProcess 0 0 1 1 0->1 λ₀ 1->0 μ₁ 2 2 1->2 λ₁ 2->1 μ₂ 3 3 2->3 λ₂ 3->2 μ₃ 4 4 3->4 λ₃ 4->3 μ₄

ノート出生死滅過程とマルコフ連鎖

出生死滅過程はマルコフ連鎖の一種である．

22.3 定常状態

時間区間 [0, t] において，状態 n に入る回数を E_n(t)，状態 n から出る回数を L_n(t) とする．このとき， |E_n(t) - L_n(t)| \leq 1 が成り立つ．これを t で割ると， \left| \frac{E_n(t)}{t} - \frac{L_n(t)}{t} \right| \leq \frac{1}{t} となる．t \to \infty とすると，

\lim_{t \to \infty} \frac{E_n(t)}{t} - \lim_{t \to \infty} \frac{L_n(t)}{t} = 0 が得られる．すなわち，t \to \infty としたとき，状態 n (n = 0, 1, 2, \ldots) において，E_n(t)/t と L_n(t)/t は等しくなる．

システムの状態が n である確率を \pi_n とするとき，

\begin{align*} \pi_0 \lambda_0 & = \pi_1 \mu_1 \\ \pi_1 (\lambda_1 + \mu_1) & = \pi_0 \lambda_0 + \pi_2 \mu_2 \\ \pi_2 (\lambda_2 + \mu_2) & = \pi_1 \lambda_1 + \pi_3 \mu_3 \\ & \vdots \end{align*}

が成り立つ．これらの式は，一般に次のようにまとめられる．

\begin{align*} \pi_0 \lambda_0 & = \pi_1 \mu_1 & \\ \pi_n (\lambda_n + \mu_n) & = \pi_{i-1} \lambda_{i-1} + \pi_{i+1} \mu_{i+1} & (i = 1, 2, \ldots) \end{align*}

これらの方程式を大域平衡方程式（global balance equation）と呼ぶ．

さらに，\pi_0 \lambda_0 = \pi_1 \mu_1 を \pi_1 (\lambda_1 + \mu_1) = \pi_0 \lambda_0 + \pi_2 \mu_2 に代入して整理すると，\pi_1 \lambda_1 = \pi_2 \mu_2 が得られる．同様にして，他の状態についてもこのような変形を行うと，一般に，

\pi_n \lambda_n = \pi_{n+1} \mu_{n+1}, \quad (n = 0, 1, 2, \ldots) が得られる．これらの方程式を局所平衡方程式（local balance equation）と呼ぶ．

局所平衡方程式より，n \geq 1 に対して，すべての \pi_n は \pi_0 を用いて次のように表される．

\pi_n = \pi_0 \frac{\lambda_0 \lambda_1 \cdots \lambda_{n-1}}{\mu_1 \mu_2 \cdots \mu_n}, \quad (n = 1, 2, \ldots)

また，\sum_{n=0}^{\infty} \pi_n = 1 であるから，

\begin{align*} \sum_{n=0}^{\infty} \pi_n & = \pi_0 + \sum_{n=1}^{\infty} \pi_n \\ & = \pi_0 + \sum_{n=1}^{\infty} \pi_0 \frac{\lambda_0 \lambda_1 \cdots \lambda_{n-1}}{\mu_1 \mu_2 \cdots \mu_n} \\ & = \pi_0 \left( 1 + \sum_{n=1}^{\infty} \frac{\lambda_0 \lambda_1 \cdots \lambda_{n-1}}{\mu_1 \mu_2 \cdots \mu_n} \right) = 1 \end{align*}

が得られる．これにより，\pi_0 は次のように与えられる．

\pi_0 = \left( 1 + \sum_{n=1}^{\infty} \frac{\lambda_0 \lambda_1 \cdots \lambda_{n-1}}{\mu_1 \mu_2 \cdots \mu_n} \right)^{-1}

これで，任意の n \geq 0 に対して，\pi_n を計算できる．

22.4 評価指標

出生死滅過程に基づいた待ち行列モデルにおいて，状態はシステム内の客数を表す．すなわち，\pi_n は系内客数が n 人である確率を表す．

平均系内客数 \mathbb{E}(L)，平均待ち行列長 \mathbb{E}(L_q) は，それぞれ次のように与えられる．

\mathbb{E}[L] = \sum_{n=0}^{\infty} n \pi_n, \quad \mathbb{E}[L_q] = \sum_{n=c}^{\infty} (n - c) \pi_n.

平均滞在時間 \mathbb{E}[W]，平均待ち時間 \mathbb{E}[W_q] は，リトルの法則により，次のように与えられる． \mathbb{E}[W] = \frac{\mathbb{E}[L]}{\bar{\lambda}}, \quad \mathbb{E}[W_q] = \frac{\mathbb{E}[L_q]}{\bar{\lambda}},

ここで，\bar{\lambda} は平均到着率であり， \bar{\lambda} = \sum_{n=0}^{\infty} \lambda_n \pi_n で与えられる．

22.5 M/M/1 モデル

M/M/1 モデルを考える．到着間隔が指数分布に従い，平均到着率が \lambda である．サービス時間も指数分布に従い，平均サービス率が \mu である．サーバ数は1である．

M/M/1 モデルを出生死滅過程として表すと，すべての状態において，出生率が \lambda，死滅率が \mu となる．すなわち，M/M/1 モデルは n \geq 0 に対して，\lambda_n = \lambda，\mu_n = \mu で表される出生死滅過程である．

22.5.1 M/M/1 モデルの定常状態

M/M/1 モデルにおいて，\rho = \lambda / \mu < 1 のとき，定常状態が存在する．このとき，\pi_0 は \pi_0 = \left( 1 + \sum_{n=1}^{\infty} \frac{\lambda^n}{\mu^n} \right)^{-1} = \left( 1 + \sum_{n=1}^{\infty} \rho^n \right)^{-1} = \left( 1 + \frac{\rho}{1-\rho} \right)^{-1} = 1 - \rho

で与えられる．

ノート等比級数の和

|x| < 1 に対して，次の式が成り立つ．

\sum_{n=0}^{\infty} x^n = \frac{1}{1-x} \quad (|x| < 1)

これを用いると，

\sum_{n=1}^{\infty} x^n = \sum_{n=0}^{\infty} x^n - 1 = \frac{1}{1-x} - 1 = \frac{x}{1-x} \quad (|x| < 1)

が得られる．

\pi_0 を用いて，任意の n \geq 0 に対して， \pi_n = \pi_0 \frac{\lambda^n}{\mu^n} = (1 - \rho) \rho^n, \quad (n = 0, 1, 2, \ldots) が得られる．

結論として，M/M/1 モデルにおいて，\rho = \lambda / \mu < 1 のとき，\pi_n は \pi_n = (1 - \rho) \rho^n, \quad (n = 0, 1, 2, \ldots) である．

22.5.2 M/M/1 モデルの評価指標

M/M/1 モデルにおける平均系内客数 \mathbb{E}[L] は次のように計算される．

\begin{align*} \mathbb{E}[L] & = \sum_{n=0}^{\infty} n \pi_n \\ & = \sum_{n=0}^{\infty} n (1 - \rho) \rho^n \\ & = (1 - \rho) \sum_{n=0}^{\infty} n \rho^n \\ & = (1 - \rho) \cdot \frac{\rho}{(1 - \rho)^2} \\ & = \frac{\rho}{1 - \rho} \\ & = \frac{\lambda}{\mu - \lambda} \end{align*}

ノート級数の和の導出

\sum_{n=0}^{\infty} n \rho^n = \frac{\rho}{(1 - \rho)^2} の導出を示す．

\begin{align*} \sum_{n=0}^{\infty} n x^n & = x + 2x^2 + 3x^3 + \cdots \\ & = x (1 + 2x + 3x^2 + \cdots) \\ & = x \sum_{n=1}^{\infty} n x^{n-1} \\ & = x \sum_{n=1}^{\infty} \frac{d}{dx} x^n \\ & = x \frac{d}{dx} \sum_{n=1}^{\infty} x^n \\ & = x \frac{d}{dx} \left(\frac{x}{1-x}\right) \\ & = x \cdot \frac{1}{(1-x)^2} \\ & = \frac{x}{(1-x)^2} \end{align*}

同様にして，平均待ち行列長 \mathbb{E}[L_q] は次のように計算される．

\begin{align*} \mathbb{E}[L_q] & = \sum_{n=1}^{\infty} (n - 1) \pi_n \\ & = \sum_{n=1}^{\infty} n \pi_n - \sum_{n=1}^{\infty} \pi_n \\ & = \mathbb{E}[L] - (1 - \pi_0) \\ & = \frac{\rho}{1 - \rho} - \rho \\ & = \frac{\rho^2}{1 - \rho} \\ & = \frac{\lambda^2}{\mu (\mu - \lambda)} \end{align*}

ノート計算に用いた関係式

ここでは， \sum_{n=1}^{\infty} n \pi_n = \sum_{n=0}^{\infty} n \pi_n = \mathbb{E}[L] および， \sum_{n=1}^{\infty} \pi_n = 1 - \pi_0 = 1 - (1 - \rho) = \rho を用いている．

M/M/1 モデルにおける平均滞在時間 \mathbb{E}[W]，平均待ち時間 \mathbb{E}[W_q] は，リトルの法則により，次のように与えられる． \mathbb{E}[W] = \frac{\mathbb{E}[L]}{\lambda} = \frac{1}{\mu - \lambda}, \quad \mathbb{E}[W_q] = \frac{\mathbb{E}[L_q]}{\lambda} = \frac{\lambda}{\mu (\mu - \lambda)}

ノートM/M/1 モデル

M/M/1 モデルにおいて，\rho = \lambda / \mu < 1 のとき，\mathbb{E}[L]，\mathbb{E}[L_q]，\mathbb{E}[W]，\mathbb{E}[W_q] はそれぞれ次のように与えられる． \mathbb{E}[L] = \frac{\rho}{1 - \rho} = \frac{\lambda}{\mu - \lambda}, \mathbb{E}[L_q] = \frac{\rho^2}{1 - \rho} = \frac{\lambda^2}{\mu (\mu - \lambda)}, \mathbb{E}[W] = \frac{1}{\mu - \lambda}, \mathbb{E}[W_q] = \frac{\lambda}{\mu (\mu - \lambda)}.

下図は，M/M/1 モデルにおける利用率 \rho と平均系内客数 \mathbb{E}[L] の関係を示している．

コード 
# rho vs L plot for M/M/1 model
import numpy as np
import matplotlib.pyplot as plt

rho = np.linspace(0.01, 0.99, 100)
L = rho / (1 - rho)
plt.plot(rho, L, c="#16212d")
plt.ylim(0, 50)
plt.xlim(0, 1.0)
plt.xlabel("Utilization ρ")
plt.ylabel("Average number of customers in system L")
# plt.grid()
plt.show()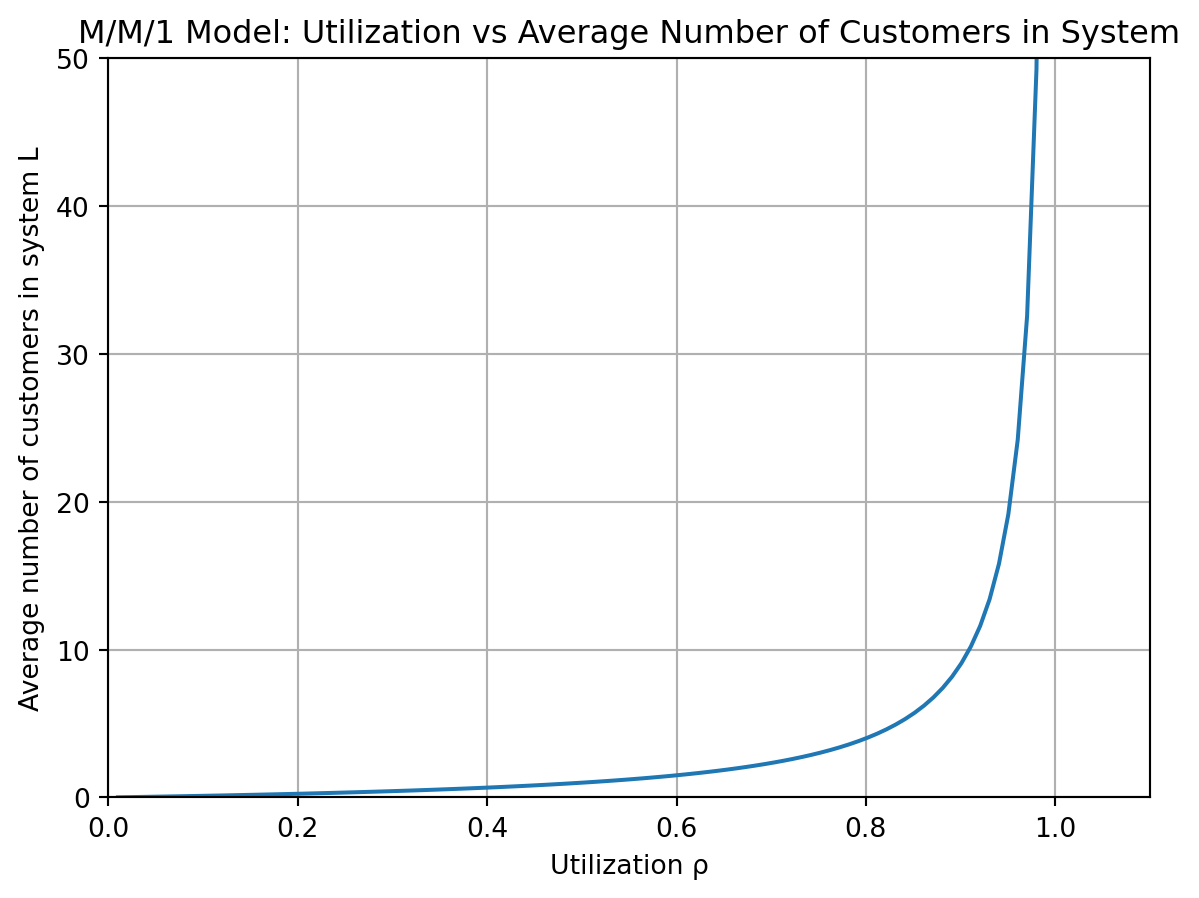

22.6 まとめ

  • 出生死滅過程では，状態遷移は隣接する状態間でのみ発生する．状態 n から n+1 への遷移確率を \lambda_n，状態 n から n-1 への遷移確率を \mu_n と表す．
  • 定常状態では，各状態に入る回数と出る回数が等しくなり，大域平衡方程式が成り立つ．これを整理すると局所平衡方程式 \pi_n \lambda_n = \pi_{n+1} \mu_{n+1} が得られる．
  • 局所平衡方程式からすべての \pi_n を \pi_0 で表し，\sum_{n=0}^{\infty} \pi_n = 1 から \pi_0 を定める．
  • 待ち行列モデルでは \pi_n は系内客数が n である確率を表し，\mathbb{E}[L] = \sum_{n} n \pi_n などで評価指標を求める．平均滞在時間はリトルの法則から得られる．
  • M/M/1 モデルは，すべての n で \lambda_n = \lambda，\mu_n = \mu である出生死滅過程である．\rho = \lambda/\mu < 1 のとき，\pi_n = (1 - \rho)\rho^n，\mathbb{E}[L] = \frac{\rho}{1 - \rho}，\mathbb{E}[L_q] = \frac{\rho^2}{1 - \rho}，\mathbb{E}[W] = \frac{1}{\mu - \lambda}，\mathbb{E}[W_q] = \frac{\lambda}{\mu(\mu - \lambda)} である．

22.7 文献案内

Bertsekas と Tsitsiklis (2008年) の「Introduction to Probability」では，確率過程とマルコフ連鎖を含めた確率論の基礎が解説されている．

もっと詳しく待ち行列理論を学びたい場合は，Shortle ほか (2018年) の「Fundamentals of Queueing Theory」が参考になる．

22.8 練習問題

練習 22.1 (理髪店) 理容師のAさんとBさんがいる理髪店を考える．n = 0, 1, 2, 3, 4 に対して，\pi_0 = 1/16，\pi_1 = 4/16，\pi_2 = 6/16，\pi_3 = 4/16，\pi_4 = 1/16 であるとする．

  1. \mathbb{E}[L] を求めよ．
  2. \mathbb{E}[L_q] を求めよ．
  3. \lambda = 4 人/時間であるとき，\mathbb{E}[W] と \mathbb{E}[W_q] を求めよ．
  4. S をサービス時間とするとき，\mathbb{E}[S] を求めよ．

解答 22.1. \mathbb{E}[L] = \sum_{n=0}^4 n \pi_n = 0 \pi_0 + 1 \pi_1 + 2 \pi_2 + 3 \pi_3 + 4 \pi_4 = 2

\mathbb{E}[L_q] = \sum_{n=2}^4 (n - 2) \pi_n = 0 \pi_2 + 1 \pi_3 + 2 \pi_4 = 0.375

\mathbb{E}[W] = \frac{\mathbb{E}[L]}{\lambda} = \frac{2}{4} = 0.5 \text{ 時間} = 30 \text{ 分}

\mathbb{E}[W_q] = \frac{\mathbb{E}[L_q]}{\lambda} = \frac{0.375}{4} = 0.09375 \text{ 時間} = 5.625 \text{ 分}

\mathbb{E}[S] = \mathbb{E}[W] - \mathbb{E}[W_q] = 0.5 - 0.09375 = 0.40625 \text{ 時間} = 24.375 \text{ 分}

練習 22.2 (ハンバーガー店) あるハンバーガー店では，店員が1人である．客の到着間隔とサービス時間はともに指数分布に従う．客の平均到着率が \lambda = 0.75 人/分，平均サービス率が \mu = 1 人/分であるとする．以下の問いに答えよ．

  1. このハンバーガー店の利用率を求めよ．
  2. 平均何人が店内にいるかを求めよ．
  3. 平均何人が待ち行列にいるかを求めよ．
  4. 客の平均滞在時間を求めよ．
  5. 客の平均待ち時間を求めよ．

解答 22.2.

  1. 利用率 \rho は，\rho = \lambda / \mu = 0.75 / 1 = 0.75 である．
  2. 平均系内客数 \mathbb{E}[L] は，\mathbb{E}[L] = \rho / (1 - \rho) = 0.75 / (1 - 0.75) = 3 である．
  3. 平均待ち行列長 \mathbb{E}[L_q] は，\mathbb{E}[L_q] = \rho^2 / (1 - \rho) = 0.75^2 / (1 - 0.75) = 2.25 である．
  4. 平均滞在時間 \mathbb{E}[W] は，\mathbb{E}[W] = 1 / (\mu - \lambda) = 1 / (1 - 0.75) = 4 分である．
  5. 平均待ち時間 \mathbb{E}[W_q] は，\mathbb{E}[W_q] = \lambda / (\mu (\mu - \lambda)) = 0.75 / (1 (1 - 0.75)) = 3 分である．