14  モデルの精度

回帰モデルの精度を評価するには，以下の指標を用いることが一般的である。

14.1 残差標準誤差

回帰モデルには，誤差項 \(\epsilon\) が含まれている．RSE は，この誤差項の標準偏差を推定するものであり，以下の式で計算される。

\[ \text{RSE} = \sqrt{\frac{1}{n - p - 1} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2} = \sqrt{\frac{\text{RSS}}{n - p - 1}} \]

\(p\) は説明変数の数を表す．単回帰分析の場合，\(p=1\) である。RSS （残差平方和; Residual Sum of Squares）は以下の式で計算される。

\[ \text{RSS} = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]

RSE が小さいほど，モデルの予測が観測値に近いことを示す．

RSE は，モデルの精度を評価するために用いられるが，\(Y\) のスケールに依存するため，決定係数がよく用いられる。

14.2 決定係数

決定係数 \(R^2\) は，モデルの精度を評価するための指標であり，0 から 1 の範囲で値を取る．

\(R^2\) は以下の式で計算される。

\[ R^2 = \frac{\text{TSS} - \text{RSS}}{\text{TSS}} \]

TSS （総平方和; Total Sum of Squares）は以下の式で計算される。

\[ \text{TSS} = \sum_{i=1}^{n} (y_i - \bar{y})^2 \]

TSS は，観測値 \(y_i\) とその平均 \(\bar{y}\) のばらつきを表す．\(\text{TSS} - \text{RSS}\) は，モデルが説明できるばらつきを表す．

すべての \(i\) について \(\hat{y}_i = y_i\) の場合，\(\text{RSS} = 0\) となり，\(R^2 = 1\) となる．一方，すべての \(i\) について \(\hat{y}_i = \bar{y}\) の場合，\(\text{RSS} = \text{TSS}\) となり，\(R^2 = 0\) となる．

\(R^2\) が 1 に近いほど，モデルの精度が高いことを示す．\(R^2\) が 0 に近い場合，モデルの精度が低いことを示す．

14.3 実装

import numpy as np

def calculate_rse(y_true, y_pred, p):
    n = len(y_true)
    rss = np.sum((y_true - y_pred) ** 2)
    rse = np.sqrt(rss / (n - p - 1))
    return rse

def calculate_r2(y_true, y_pred):
    tss = np.sum((y_true - np.mean(y_true)) ** 2)
    rss = np.sum((y_true - y_pred) ** 2)
    r2 = (tss - rss) / tss
    return r2

14.4 Python による計算例

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt

# サンプルデータの生成
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 線形回帰モデルの学習
model = LinearRegression()
model.fit(X, y)

# plot
plt.scatter(X, y, color="blue")
plt.plot(X, model.predict(X), color="red")
plt.xlabel("X")
plt.ylabel("y")
plt.show()

# 決定係数の計算
r2 = r2_score(y, model.predict(X))
print(f"決定係数 R^2: {r2}")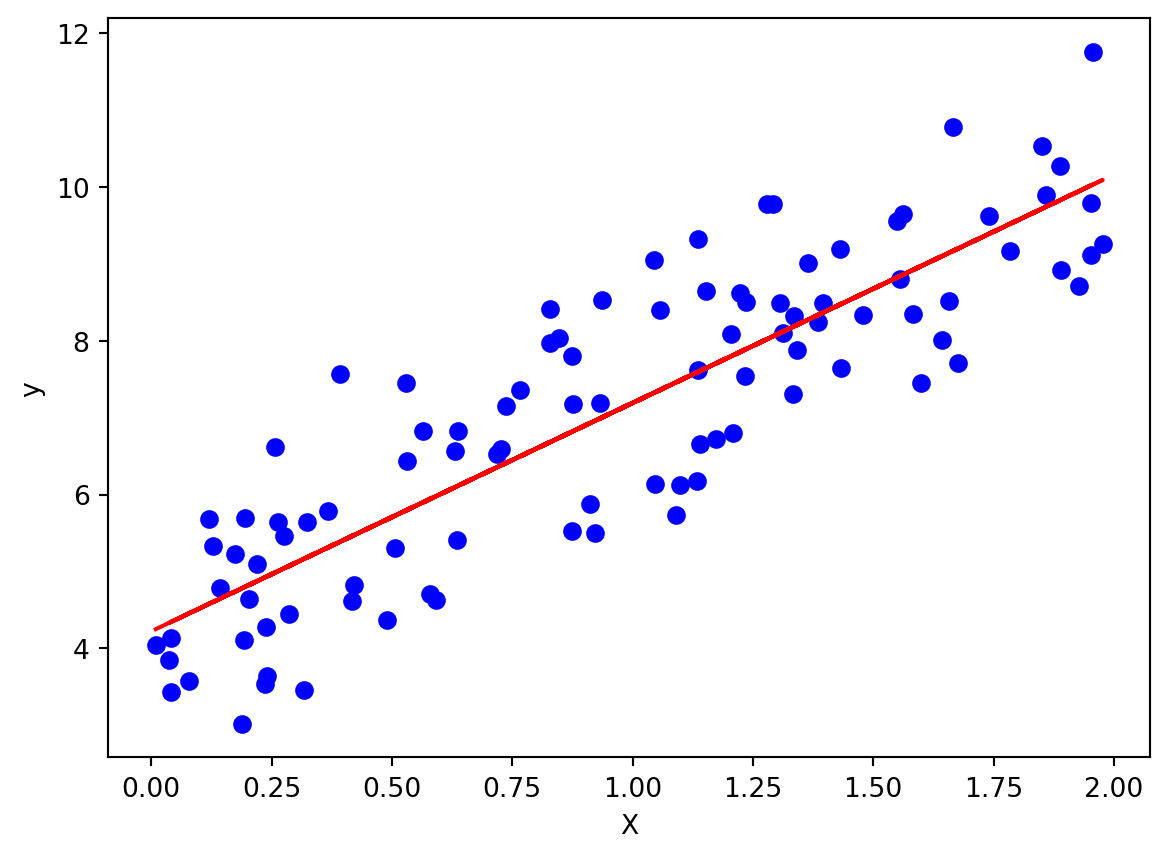

決定係数 R^2: 0.7469629925504755
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt

# サンプルデータの生成
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + 0.1 * np.random.randn(100, 1)

# 線形回帰モデルの学習
model = LinearRegression()
model.fit(X, y)

# plot
plt.scatter(X, y, color="blue")
plt.plot(X, model.predict(X), color="red")
plt.xlabel("X")
plt.ylabel("y")
plt.show()

# 決定係数の計算
r2 = r2_score(y, model.predict(X))
print(f"決定係数 R^2: {r2}")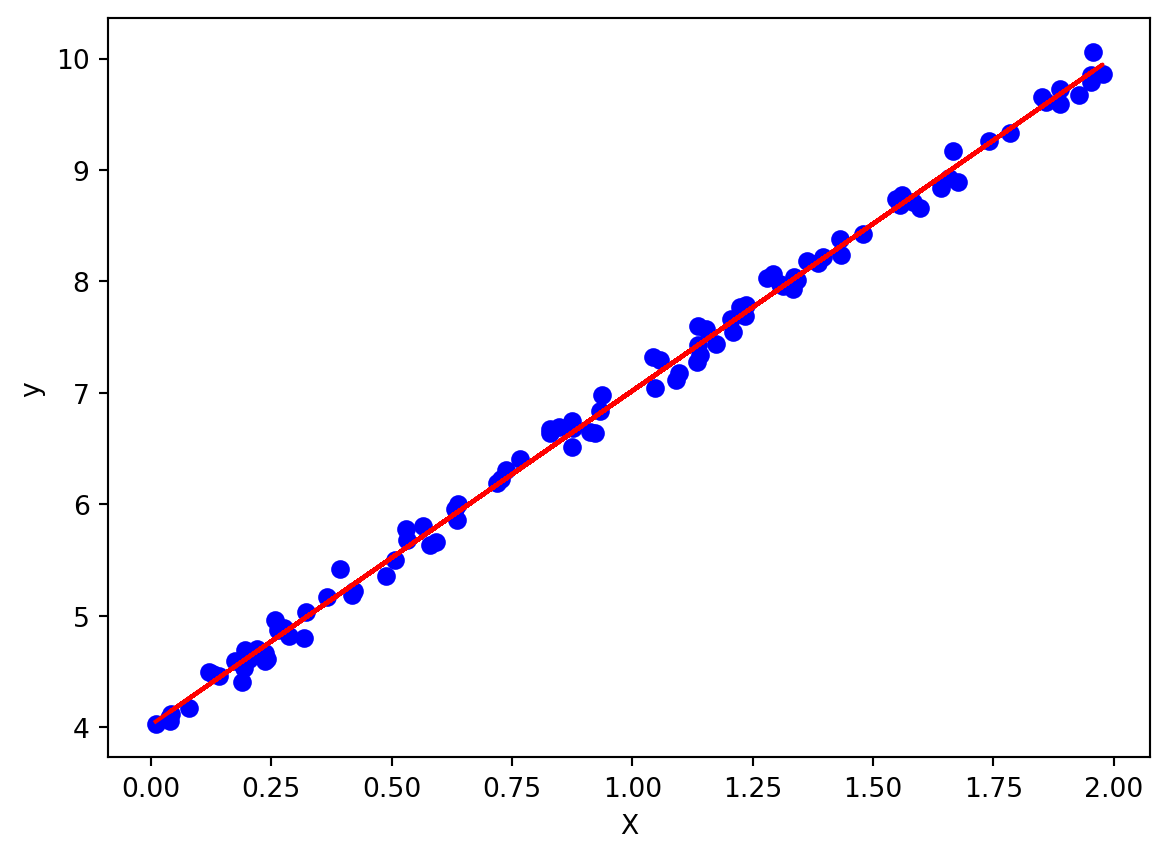

決定係数 R^2: 0.9966873204996887