二値分類
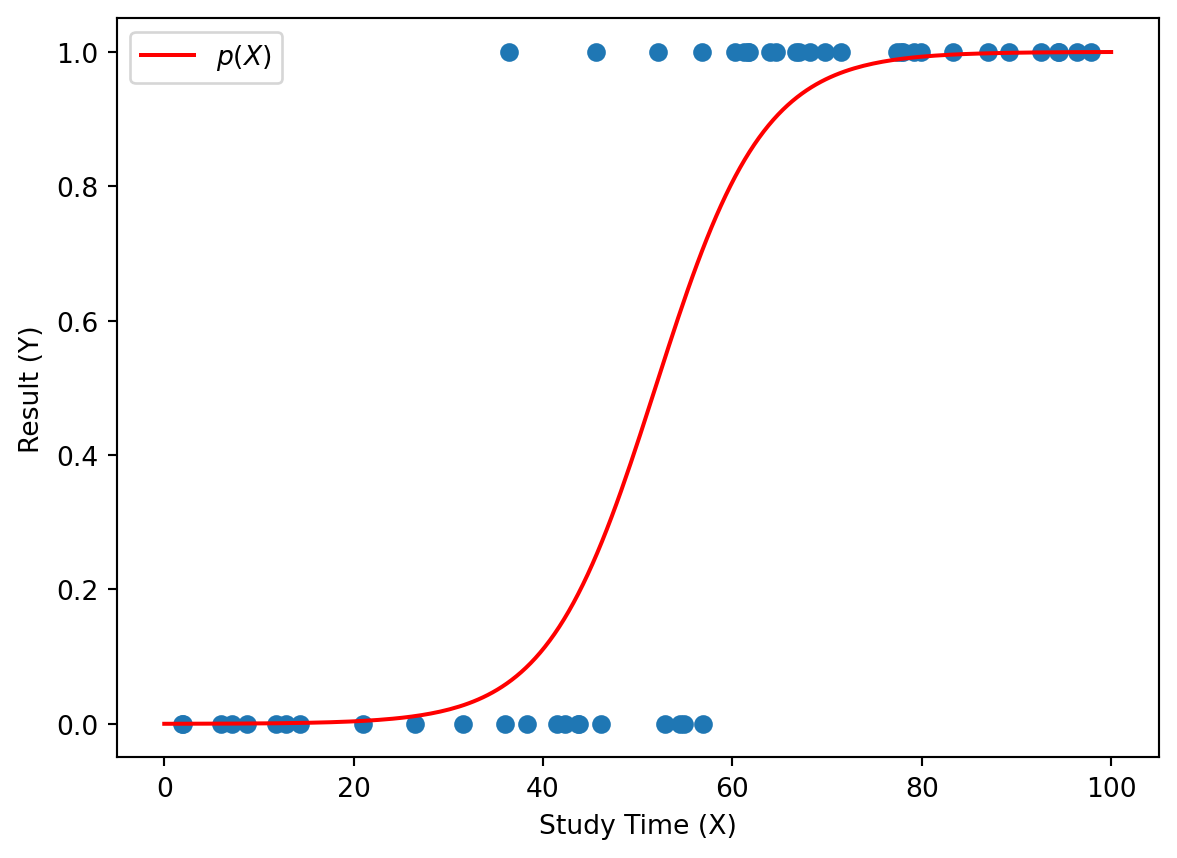
50人の学生がある試験を受けた。各学生の勉強時間を \(X\),試験の合格・不合格を \(Y\) とする。ここで,\(Y\) は次のように定義される二値変数である。
\[
Y =
\begin{cases}
1 & \text{合格} \\
0 & \text{不合格}
\end{cases}
\]
下の散布図では,横軸が勉強時間 \(X\),縦軸が合格・不合格 \(Y\) を表している。
Code
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
np.random.seed(0)
X = np.random.uniform(0, 100, 50)
y = (X + np.random.normal(0, 15, 50) > 50).astype(int)
X = X.reshape(-1, 1) # Reshape for sklearn
model = LogisticRegression()
model.fit(X, y)
plt.scatter(X, y)
x_values = np.linspace(0, 100, 200).reshape(-1, 1)
y_values = model.predict_proba(x_values)[:, 1]
# latex label
plt.plot(x_values, y_values, color="red", label=f"$p(X)$")
plt.xlabel("Study Time (X)")
plt.ylabel("Result (Y)")
plt.legend()
plt.show()
ロジスティック回帰は,説明変数 \(X\) を使って,目的変数 \(Y\) の確率を予測するための手法である。例えば,ある学生が \(X=70\) 時間勉強したときに,その学生が合格する確率は \(P(Y=1|X=70)\) と表される。これ以降,この確率を \(p(X)\) と略記する。
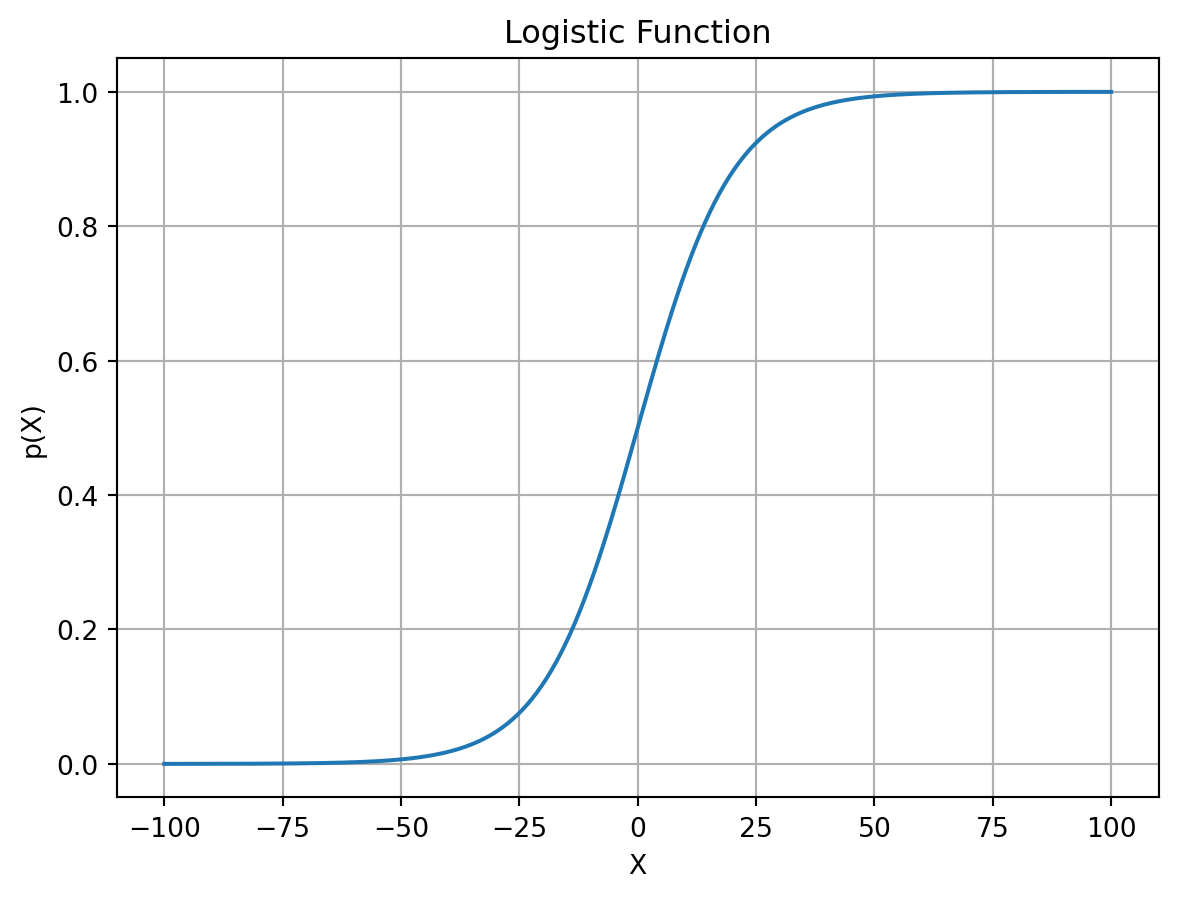
ロジスティック関数
ロジスティック関数(logistic function)は次のように表される.
\[
p(X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X)}}
\]
ここで,\(X\) は説明変数,\(\beta_0\) と \(\beta_1\) はパラメータである.ロジスティック関数は \(-\infty\) から \(\infty\) の範囲の \(X\) を入力として,\(0\) から \(1\) の範囲の確率 \(p(X)\) を出力する.
Code
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(-100, 100, 400)
beta_0 = 0
beta_1 = 0.1
p_X = 1 / (1 + np.exp(-(beta_0 + beta_1 * X)))
plt.plot(X, p_X)
plt.title("Logistic Function")
plt.xlabel("X")
plt.ylabel("p(X)")
plt.grid()
plt.show()
オッズとロジット
オッズ(odds)は、ある事象が起こる確率と起こらない確率の比率を表す. \[
\text{odds} = \frac{p(X)}{1 - p(X)}
\]
例えば,5回に1回成功する場合,成功の確率は0.2ですが,オッズは
\[
\frac{0.2}{0.8} = \frac{1}{4} = 0.25
\]
となる.
オッズは \(0\) から \(\infty\) の範囲を取り,確率 \(p(X)\) が \(0.5\) のときオッズは \(1\) になる.
ロジット(logit)はオッズの対数を取ったもので,次のように表される.
\[
\text{logit}(p(X)) = \log\left(\frac{p(X)}{1 - p(X)}\right) = \beta_0 + \beta_1 X
\]
ロジットは \(-\infty\) から \(\infty\) の範囲を取り,確率 \(p(X)\) が \(0.5\) のときロジットは \(0\) になる.
尤度関数
ロジスティック回帰モデルのパラメータ \(\beta_0\) と \(\beta_1\) を推定するために,尤度関数を最大化する.
\[
L(\beta_0, \beta_1) = \prod_{i:y_i=1} p(x_i) \prod_{i:y_i=0} (1 - p(x_i))
\]
この式は,
\[
L(\beta_0, \beta_1) = \prod_{i=1}^{n} p(x_i)^{y_i} (1 - p(x_i))^{1 - y_i}
\] で表すこともできる.
この関数の対数を取ったものを対数尤度関数と呼び,次のように表される.
\[\begin{align*}
\ell(\beta_0, \beta_1) &= \log L(\beta_0, \beta_1) \\
&= \sum_{i=1}^{n} \left[ y_i \log p(x_i) + (1 - y_i) \log (1 - p(x_i)) \right]
\end{align*}\]
\(\ell(\beta_0, \beta_1)\) を最大化する \(\beta_0\) と \(\beta_1\) を求めることは,\(-\ell(\beta_0, \beta_1)\) を最小化することと同じである.ここでは,最小化問題を考えるために,損失関数を次のように定義する.
\[
L(\beta_0, \beta_1) = - \ell(\beta_0, \beta_1) = \sum_{i=1}^{n} \left[ - y_i \log p(x_i) - (1 - y_i) \log (1 - p(x_i)) \right]
\]
勾配降下法
損失関数 \(L(\beta_0, \beta_1)\) を最小化するために,勾配降下法を用いる.損失関数の各パラメータに関する偏微分は次のようになる.
\[\begin{align*}
\frac{\partial L}{\partial \beta_0} &= \sum_{i=1}^{n} (p(x_i) - y_i) \\
\frac{\partial L}{\partial \beta_1} &= \sum_{i=1}^{n} (p(x_i) - y_i) x_i
\end{align*}\]
これらの偏微分を用いて,パラメータを更新する.学習率を \(\alpha\) とすると,更新式は次のようになる.
\[\begin{align*}
\beta_0 &\leftarrow \beta_0 - \alpha \frac{\partial L}{\partial \beta_0} \\
\beta_1 &\leftarrow \beta_1 - \alpha \frac{\partial L}{\partial \beta_1}
\end{align*}\]
scikit-learnによる実装
上記のロジスティック回帰モデルは,scikit-learn の LogisticRegression クラスを用いて簡単に実装できる.以下にその例を示す.
import numpy as np
from sklearn.linear_model import LogisticRegression
# データの生成
np.random.seed(0)
X = np.random.uniform(0, 100, 50).reshape(-1, 1)
y = (X.flatten() + np.random.normal(0, 15, 50) > 50).astype(int)
# ロジスティック回帰モデルの学習
model = LogisticRegression()
model.fit(X, y)
# パラメータの表示
print("Intercept (β0):", model.intercept_[0])
print("Coefficient (β1):", model.coef_[0][0])
Intercept (β0): -9.093527571121504
Coefficient (β1): 0.17535051335865087
\(\beta_0 \approx -9.0935\),\(\beta_1 \approx 0.1754\) が得られる.これにより,ロジスティック関数は次のようになる.
\[
p(X) = \frac{1}{1 + e^{-(-9.0935 + 0.1754 X)}}
\]
ある学生が \(X=80\) 時間勉強したときに,その学生が合格する確率は次のように計算される.
\[
p(80) = \frac{1}{1 + e^{-(-9.0935 + 0.1754 \times 80)}} \approx 0.9929
\]
Code
X_new = np.array([[80]])
prob = model.predict_proba(X_new)[0][1]
print("Probability of passing for X=80:", prob)
Probability of passing for X=80: 0.9928574234362196