import matplotlib.pyplot as plt
learn_hours = [2, 3, 4, 5, 6, 7, 8, 9, 10]
exam_scores = [52, 58, 60, 67, 72, 73, 80, 82, 89]
plt.scatter(learn_hours, exam_scores)
plt.show()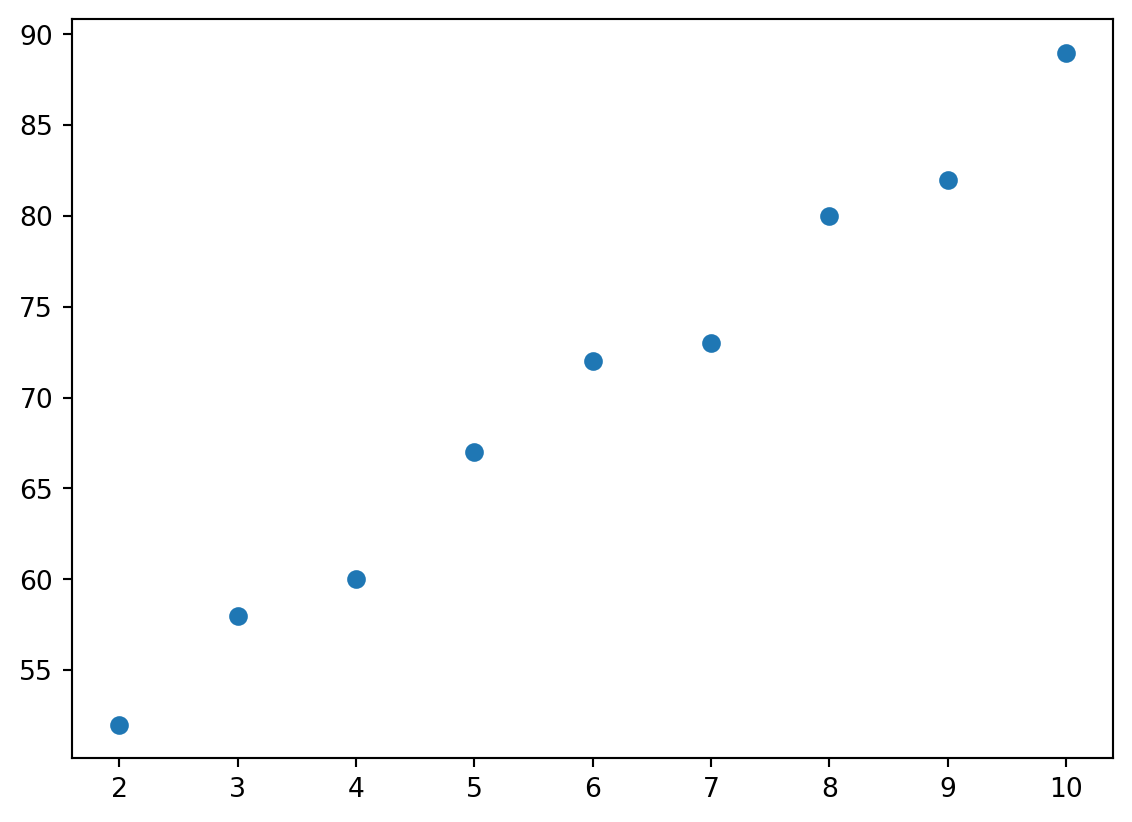
10 相関
代表値や分散を用いて一つの変数を要約する方法について述べた。ここでは、二つの変数の相関関係を分析する方法について述べる。
\(X\) と \(Y\) を二つの変数とする。\(n\) 組のデータが
\[ (x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n) \]
で与えられる。ここで，\((x_i, y_i)\) は \(i\) 番目のデータとする。
| \(i\) | \(X\) | \(Y\) |
|---|---|---|
| 1 | \(x_1\) | \(y_1\) |
| 2 | \(x_2\) | \(y_2\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(n\) | \(x_n\) | \(y_n\) |
例えば、\(X\) を身長、\(Y\) を体重とする。\(n\) 組のデータが以下のように与えられたとする。
| 身長 (cm) | 体重 (kg) | |
|---|---|---|
| 1 | 160 | 55 |
| 2 | 170 | 65 |
| 3 | 180 | 75 |
| 4 | 175 | 70 |
| 5 | 185 | 80 |
10.1 散布図
二つの変数 \(X\) と \(Y\) の関係性を視覚的に把握するために散布図を用いる。散布図は、データ \((x_i, y_i)\) を2次元の座標平面上に点で表現したものである。
Example 10.1 変数 \(X\) を勉強時間、変数 \(Y\) を「試験の点数」とする。以下のデータセットが与えられたとする。
| 勉強時間 | 試験の点数 |
|---|---|
| 2 | 52 |
| 3 | 58 |
| 4 | 62 |
| 5 | 65 |
| 6 | 70 |
| 7 | 73 |
| 8 | 80 |
| 9 | 82 |
| 10 | 89 |
Python では、matplotlib ライブラリの scatter() 関数を用いて散布図を描くことができる。scatter() 関数は、横軸と縦軸のデータをそれぞれリストとして引数に渡すことで散布図を作成する。plt.show() を用いて、描画した散布図を表示する。
この散布図から、勉強時間が増えるにつれて試験の点数も上昇する傾向があることがわかる。これは、二つの変数が正の相関があると言える。
10.2 相関係数
相関係数を紹介する前に、まずは共分散（covariance）を定義する。
10.2.1 共分散
データセット \(\{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}\) が与えられるとき、\(X\) と \(Y\) の標本共分散は \[ s_{XY} = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) \]
で定義される。
| \(x_i\) | \(y_i\) | \((x_i - \bar{x})(y_i - \bar{y})\) | |
|---|---|---|---|
| A | \(x_i > \bar{x}\) | \(y_i > \bar{y}\) | positive |
| B | \(x_i < \bar{x}\) | \(y_i > \bar{y}\) | negative |
| C | \(x_i < \bar{x}\) | \(y_i < \bar{y}\) | positive |
| D | \(x_i > \bar{x}\) | \(y_i < \bar{y}\) | negative |
Code
import numpy as np
import matplotlib.pyplot as plt
# generate random data with positive correlation
np.random.seed(0)
n = 100
x = np.random.rand(n) * 10 # x values between 0 and 10
y = 2 * x + np.random.randn(n) * 4 # y values with some noise
plt.scatter(x, y)
plt.xlabel("X")
plt.ylabel("Y")
# x and y means
x_mean = np.mean(x)
y_mean = np.mean(y)
# plot means
plt.axvline(x_mean, color="r", linestyle="--", label="Mean of X")
plt.axhline(y_mean, color="g", linestyle="--", label="Mean of Y")
# plot shaded areas
plt.fill_betweenx([y_mean, max(y)], x_mean, max(x), color="yellow", alpha=0.1)
plt.fill_betweenx([y_mean, max(y)], min(x), x_mean, color="blue", alpha=0.1)
plt.fill_betweenx([min(y), y_mean], min(x), x_mean, color="yellow", alpha=0.1)
plt.fill_betweenx([min(y), y_mean], x_mean, max(x), color="blue", alpha=0.1)
# plot A, B, C, D in the middle of each area
plt.text(
(x_mean + max(x)) / 2,
(y_mean + max(y)) / 2,
"A",
fontsize=16,
ha="center",
va="center",
)
plt.text(
(min(x) + x_mean) / 2,
(y_mean + max(y)) / 2,
"B",
fontsize=16,
ha="center",
va="center",
)
plt.text(
(min(x) + x_mean) / 2,
(min(y) + y_mean) / 2,
"C",
fontsize=16,
ha="center",
va="center",
)
plt.text(
(x_mean + max(x)) / 2,
(min(y) + y_mean) / 2,
"D",
fontsize=16,
ha="center",
va="center",
)
plt.legend()
plt.show()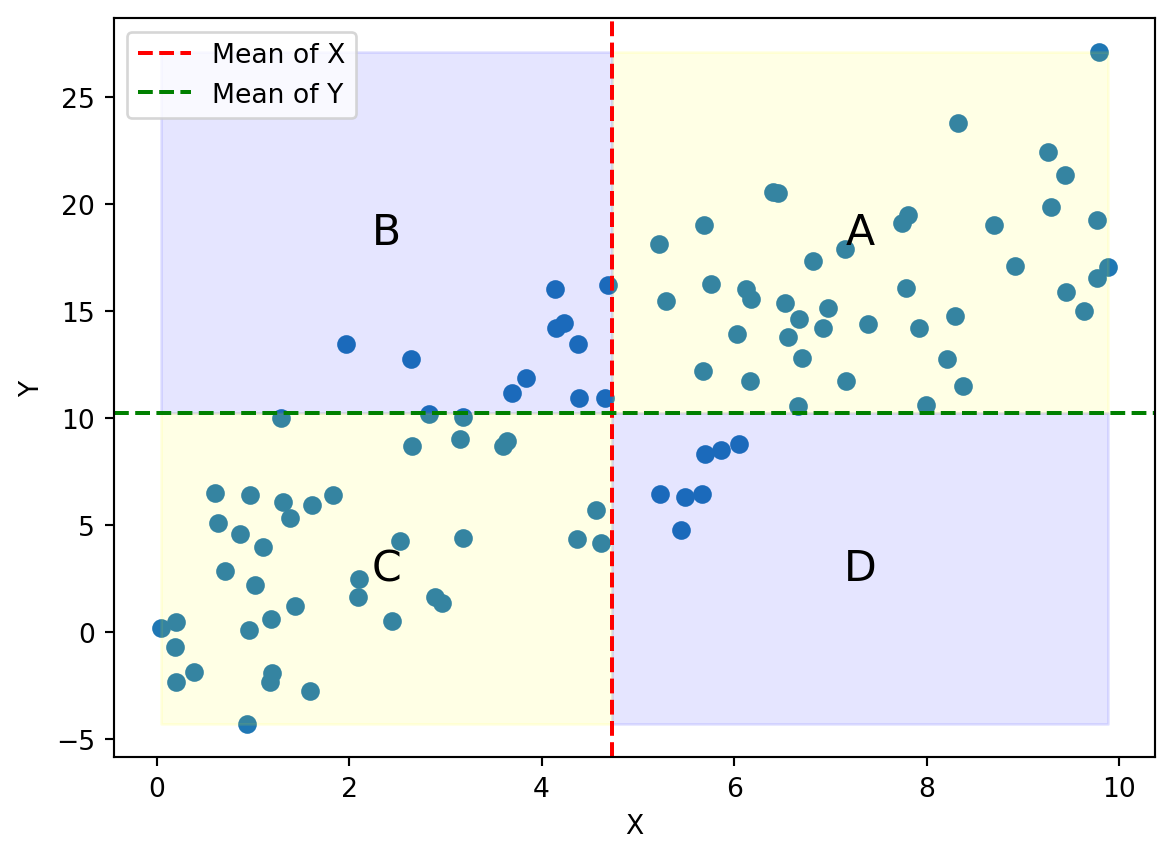
これにより、\(s_{XY} > 0\) のとき、\(X\) が増えると \(Y\) も増える傾向があり、\(s_{XY} < 0\) のとき、\(X\) が増えると \(Y\) は減る傾向があることがわかる。
共分散は、二つの変数の関係を示す指標であるが、単位に依存するという欠点がある。例えば、身長と体重の共分散は、身長がセンチメートルの場合はメートルの場合の結果の100倍になる。
import numpy as np
height_cm = np.array([170, 180, 160, 175, 185])
height_m = height_cm / 100
weight_kg = np.array([65, 75, 55, 70, 80])
cov_cm_kg = np.cov(height_cm, weight_kg, ddof=1)[0, 1]
cov_m_kg = np.cov(height_m, weight_kg, ddof=1)[0, 1]
print(f"Covariance (cm, kg): {cov_cm_kg}")
print(f"Covariance (m, kg): {cov_m_kg}")Covariance (cm, kg): 92.5
Covariance (m, kg): 0.92510.2.2 相関係数
共分散を標準偏差で割ることで、単位に依存しない指標である相関係数（correlation coefficient）を定義できる。
標本相関係数 \(r\) は以下の式で定義される。
\[ r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}} \]
変数 \(X\) の標本分散 \(s_{XX}\) と、変数 \(Y\) の標本分散 \(s_{YY}\) は以下のように定義される。
\[ s_{XX} = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2, \quad s_{YY} = \frac{1}{n-1} \sum_{i=1}^{n} (y_i - \bar{y})^2 \]
さらに、記号 \(s_{X} = \sqrt{s_{XX}}\) と \(s_{Y} = \sqrt{s_{YY}}\) を導入すると、相関係数は以下のように書ける。
\[ r = \frac{s_{XY}}{s_X s_Y} \]
相関係数は以下の性質を持つ。
- 相関係数は単位に依存しない。
- 相関係数 \(r\) は \(-1 \leq r \leq 1\) を満たす。
- \(r\) が \(1\) に近いほど、\(X\) と \(Y\) は強い正の相関がある。
- \(r\) が \(-1\) に近いほど、\(X\) と \(Y\) は強い負の相関がある。
import numpy as np
height_cm = np.array([170, 180, 160, 175, 185])
weight_kg = np.array([65, 75, 55, 70, 80])
corr = np.corrcoef(height_cm, weight_kg)[0, 1]
print(f"Correlation coefficient: {corr}")Correlation coefficient: 1.010.3 練習問題
Exercise 10.1 次のコードは，「Iris setosa」のがく片の長さ（sepal length）とがく片の幅（sepal width）のデータを読み込むものである。setosa_sepal_length にがく片の長さ、setosa_sepal_width にがく片の幅のデータが格納されている。Iris setosaのがく片の長さと幅の散布図を描き、相関係数を計算せよ。
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import numpy as np
data = load_iris(as_frame=True)
setosa = data.data[data.target == 0] # Iris setosa のデータ
setosa_sepal_length = setosa["sepal length (cm)"] # がく片の長さ
setosa_sepal_width = setosa["sepal width (cm)"] # がく片の幅
# ここにコードを書くExercise 10.2 my_corrcoef 関数を実装せよ。この関数は、二つの同じ長さのNumPy配列を引数に取り、相関係数を返すものである。
import numpy as np
def my_corrcoef(x, y):
# ここにコードを書く
return r
# 動作確認
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 8, 10])
print(my_corrcoef(x, y)) # 期待される出力: 1.0