6  確率統計

確率変数（random variable）は、試行の結果に対応して，その数値が定まる変数でそれぞれ決まった確率が与えられているものである。一般に、確率変数は大文字の \(X, Y\) などで表される。確率変数 \(X\) が取りうる値の集合を標本空間 (sample space) と呼び，\(\Omega\) と書く．

例えば，サイコロの目を表す確率変数 \(X\) の標本空間は \(\Omega = \{1, 2, 3, 4, 5, 6\}\) である．

確率変数には，離散型 (discrete) と連続型 (continuous) の 2 種類がある．

6.1 離散型確率変数

確率質量関数 (probability mass function; PMF) は，離散型確率変数が特定の値を取る確率を表す関数であり，\(f(x) = P(X = x)\) と書く．

scipy.stats モジュールを用いて，離散型確率変数を定義できる．

from scipy.stats import rv_discrete

X_values = [1, 2, 3, 4, 5, 6]
X_probs = [1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6]

X = rv_discrete(values=(X_values, X_probs))

この確率変数 \(X\) の確率質量関数を次の図に示す．

Code 
import matplotlib.pyplot as plt

x = X_values
y = X.pmf(x)

plt.stem(x, y, basefmt=" ")
plt.xlabel("x")
plt.ylabel("P(X = x)")
plt.ylim(0, 0.2)
plt.title("Probability Mass Function")
plt.show()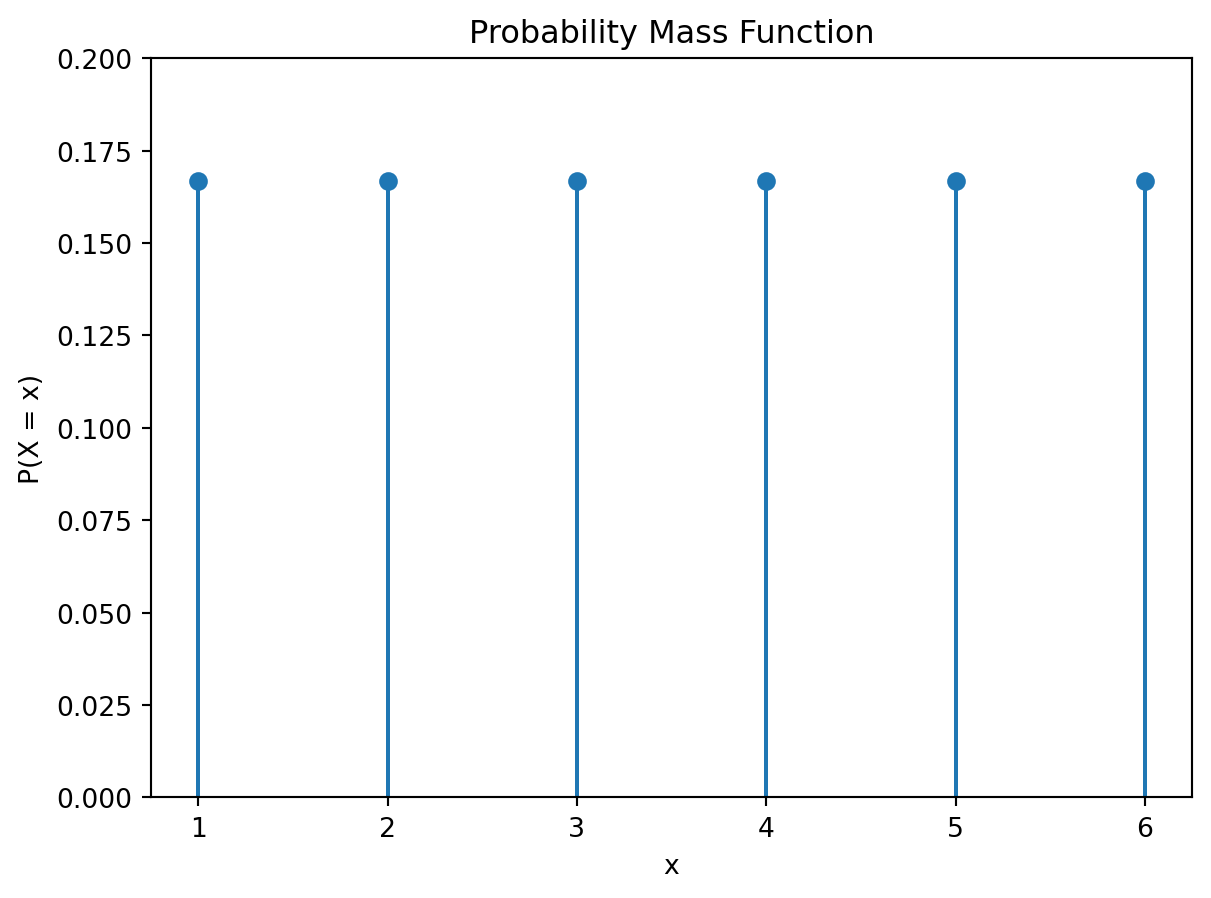

例えば，\(P(X = 3)\) を計算するには，次のようにする．

print(X.pmf(3))
0.16666666666666666

累積分布関数 (cumulative distribution function; CDF) は，確率変数が特定の値以下を取る確率を表す関数であり，\(F(x) = P(X \leq x)\) と書く．

累積分布関数を図に示す．

Code 
import numpy as np

x = np.arange(1, 7)
y_cdf = X.cdf(x)
plt.scatter(x, y_cdf, color="black")
plt.scatter(x + 1, y_cdf, color="white", edgecolor="black")
for i in range(len(x) - 1):
    plt.hlines(y_cdf[i], x[i], x[i + 1], colors="black")
plt.hlines(y_cdf[-1], x[-1], x[-1] + 1, colors="black")
plt.xlabel("x")
plt.ylabel("P(X ≤ x)")
plt.ylim(0, 1.2)
plt.title("Cumulative Distribution Function")
plt.grid()
plt.show()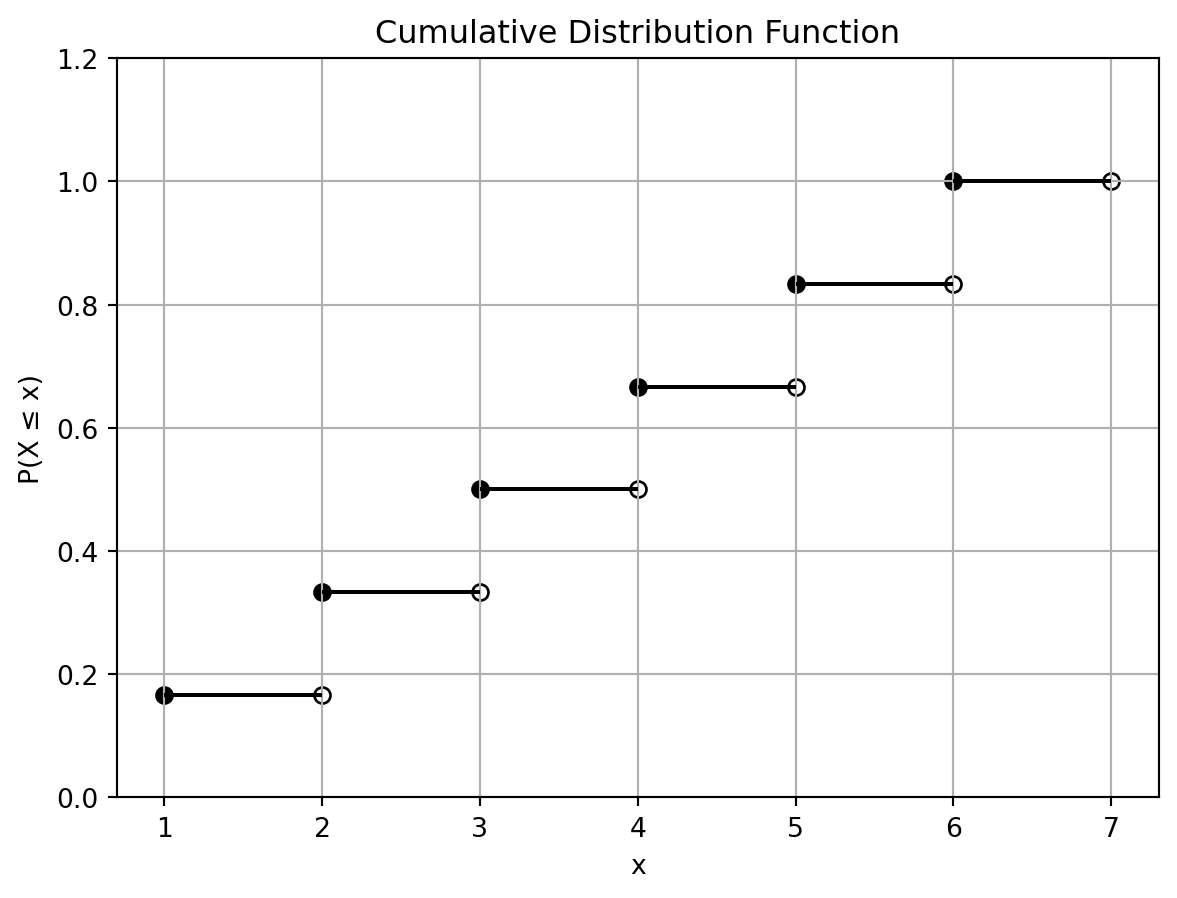

例えば，\(P(X \leq 3)\) を計算するには，次のようにする．

print(X.cdf(3))
0.5

6.2 連続型確率変数

確率密度関数 (probability density function; PDF) は，連続型確率変数が特定の値を取る確率密度を表す関数であり，\(f(x)\) と書く．

連続型確率変数の場合，特定の値を取る確率は 0 であるため，確率密度関数を用いて区間の確率を計算する．例えば，\(P(a \leq X \leq b)\) は次のように計算される．

\[ P(a \leq X \leq b) = \int_{a}^{b} f(x) \, dx \]

scipy.stats モジュールを用いて，様々な連続型確率変数を定義できる．

ここでは，\(X \sim N(0, 1)\) として，\(X\) を標準正規分布に従う確率変数とする．

from scipy.stats import norm

X = norm(loc=0, scale=1)

この確率変数 \(X\) の確率密度関数を次の図に示す．

Code 
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-4, 4, 100)
y = X.pdf(x)

plt.plot(x, y, color="blue")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("Probability Density Function")
plt.grid()
plt.show()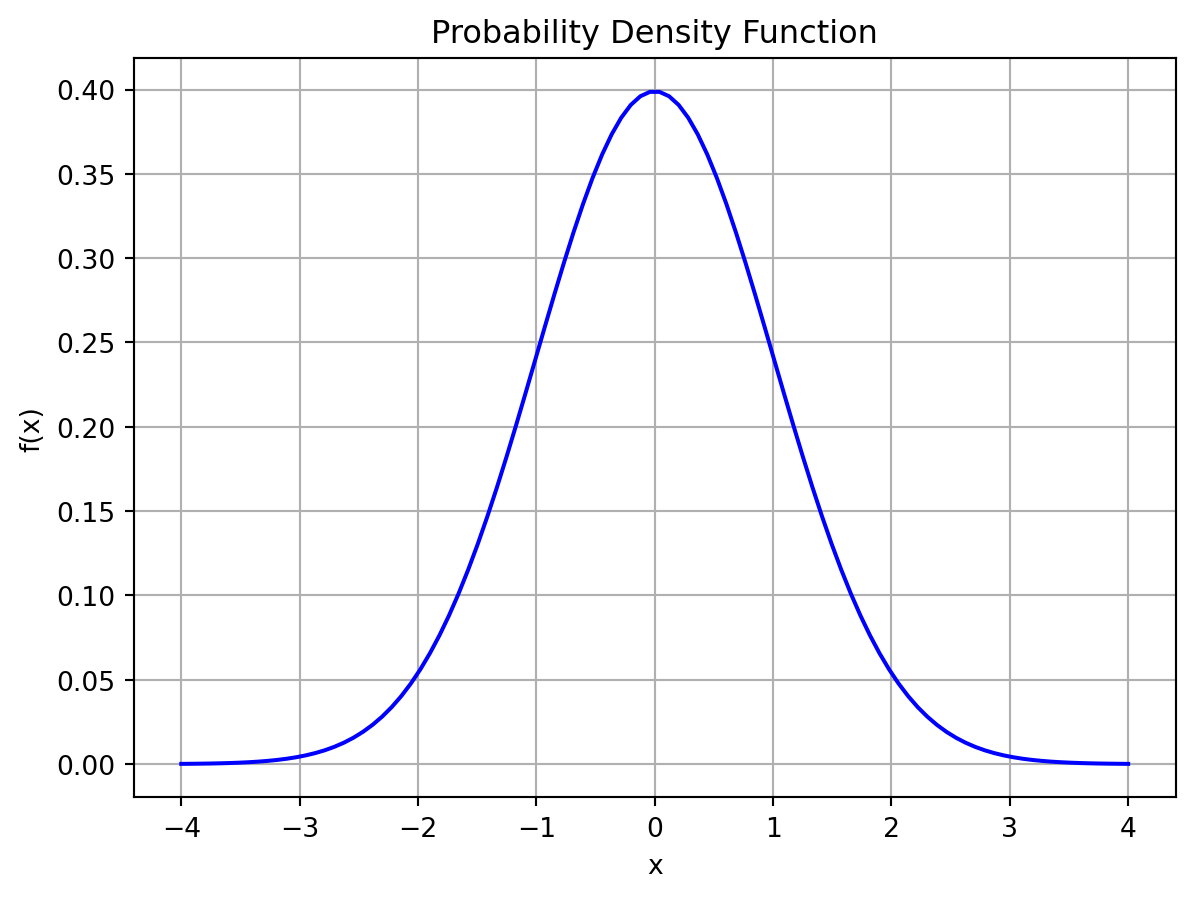

標準正規分布の累積分布関数を \(\Phi(x) = P(X \leq x)\) と書く．例えば，\(P(X \leq 1.96)\) は次のように計算される．

print(X.cdf(1.96))
0.9750021048517795
Code 
# draw CDF
x = np.linspace(-4, 4, 1000)
y = X.pdf(x)

plt.plot(x, y, color="blue")
plt.fill_between(x, 0, y, where=(x <= 1.96), color="lightblue", alpha=0.5)
plt.axvline(1.96, color="red", linestyle="--")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("Probability Density Function")
plt.grid()
plt.show()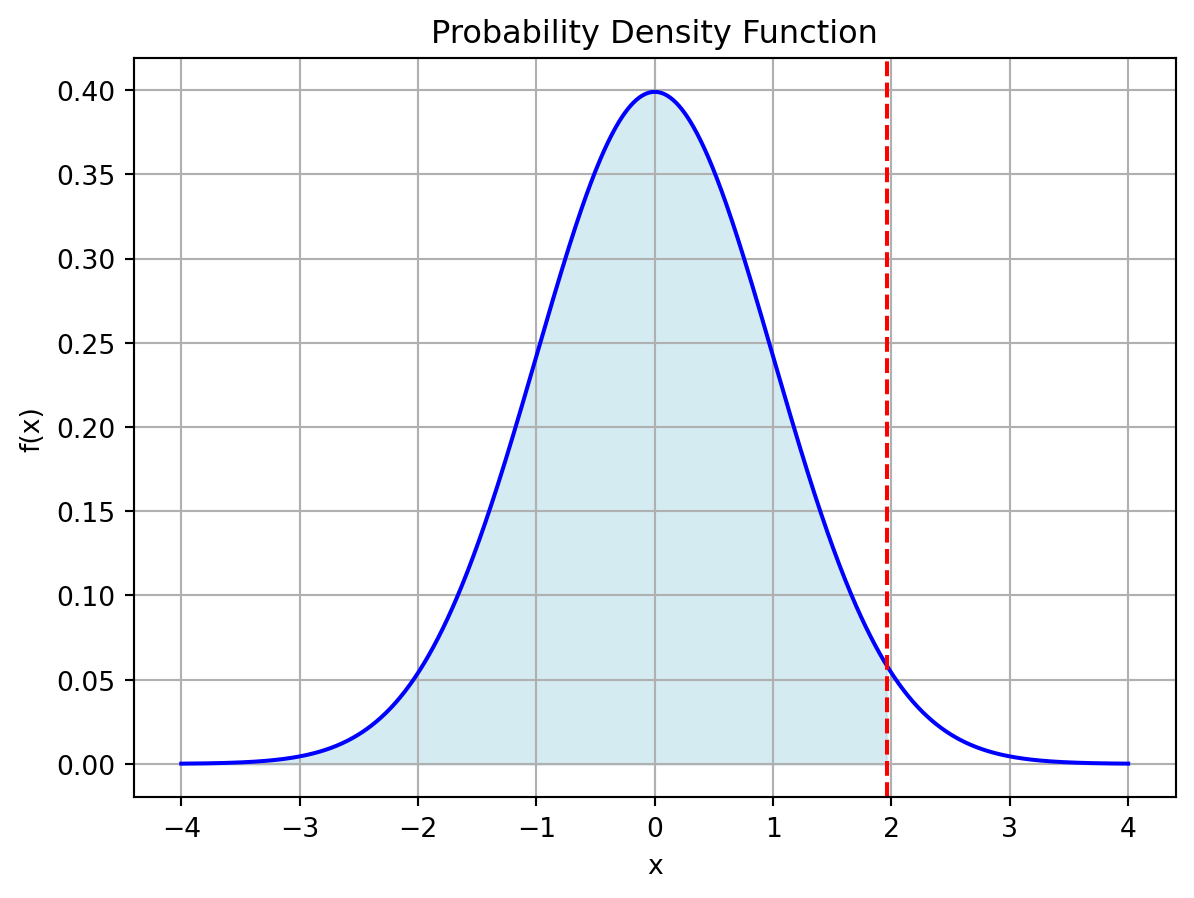

標準正規分布の累積分布関数を図に示す．

Code 
y_cdf = X.cdf(x)
plt.plot(x, y_cdf, color="blue")
plt.xlabel("x")
plt.ylabel("P(X ≤ x)")
plt.ylim(0, 1.2)
plt.title("Cumulative Distribution Function")
plt.grid()
plt.show()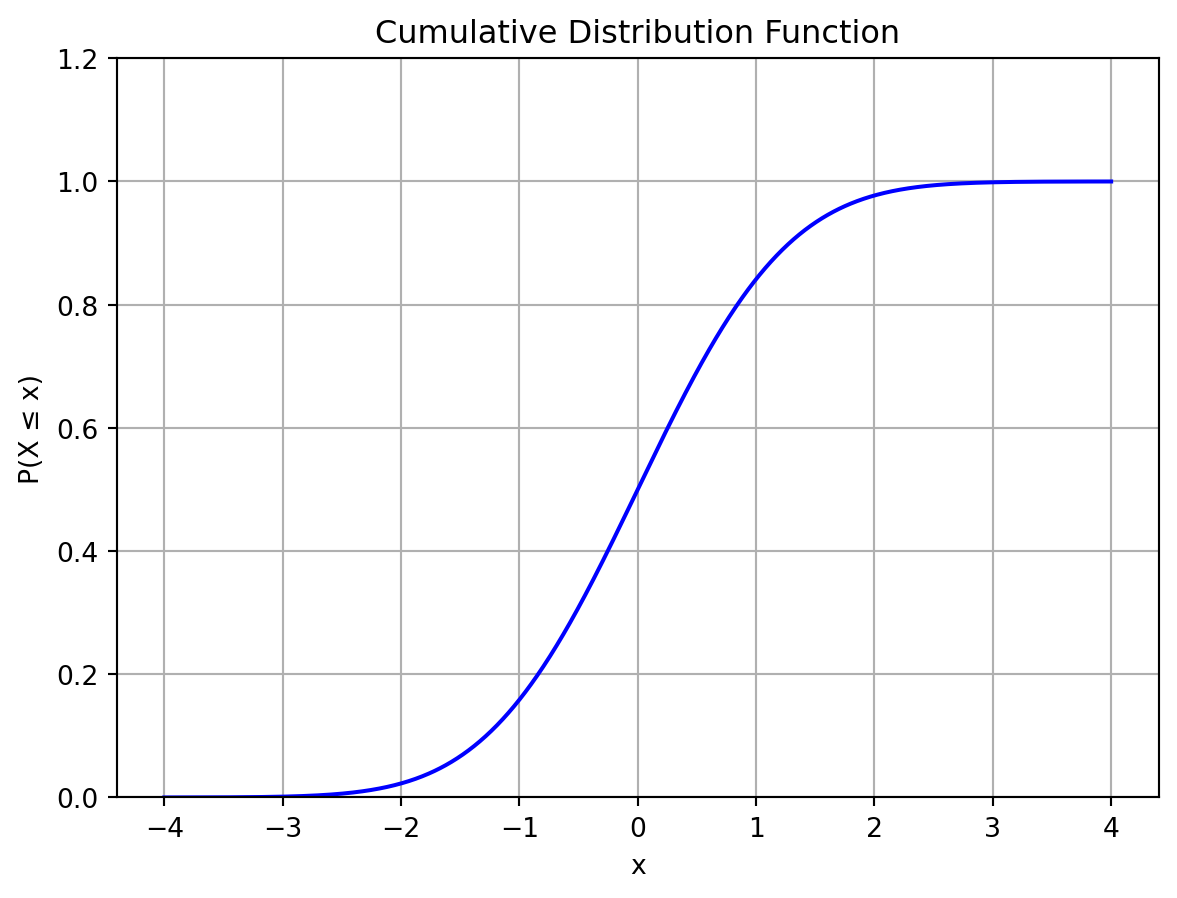

\(P(-1 \leq X \leq 1)\) は次のように計算される．

\[ P(-1 \leq X \leq 1) = \Phi(1) - \Phi(-1) \]

Python では次のように計算する．

print(X.cdf(1) - X.cdf(-1))
0.6826894921370859

6.3 母集団と標本

統計の調査対象の全体を母集団（population）といい、母集団の一部を標本（sample）という。標本はサンプルとも呼ぶ。標本の大きさを標本サイズ（sample size）といい、一般に \(n\) で表される。

\(X \sim N(0, 1)\) からサンプルを 1000 個生成するには，rvs() メソッドを用いる．

X = norm(loc=0, scale=1)
samples = X.rvs(size=1000)

これらのサンプルのヒストグラムを次の図に示す．

Code 
plt.hist(samples, bins=20, density=True, alpha=0.6, color="blue")
plt.plot(x, y, color="red")
plt.xlabel("x")
plt.ylabel("Density")
plt.title("Histogram of Samples")
plt.grid()
plt.show()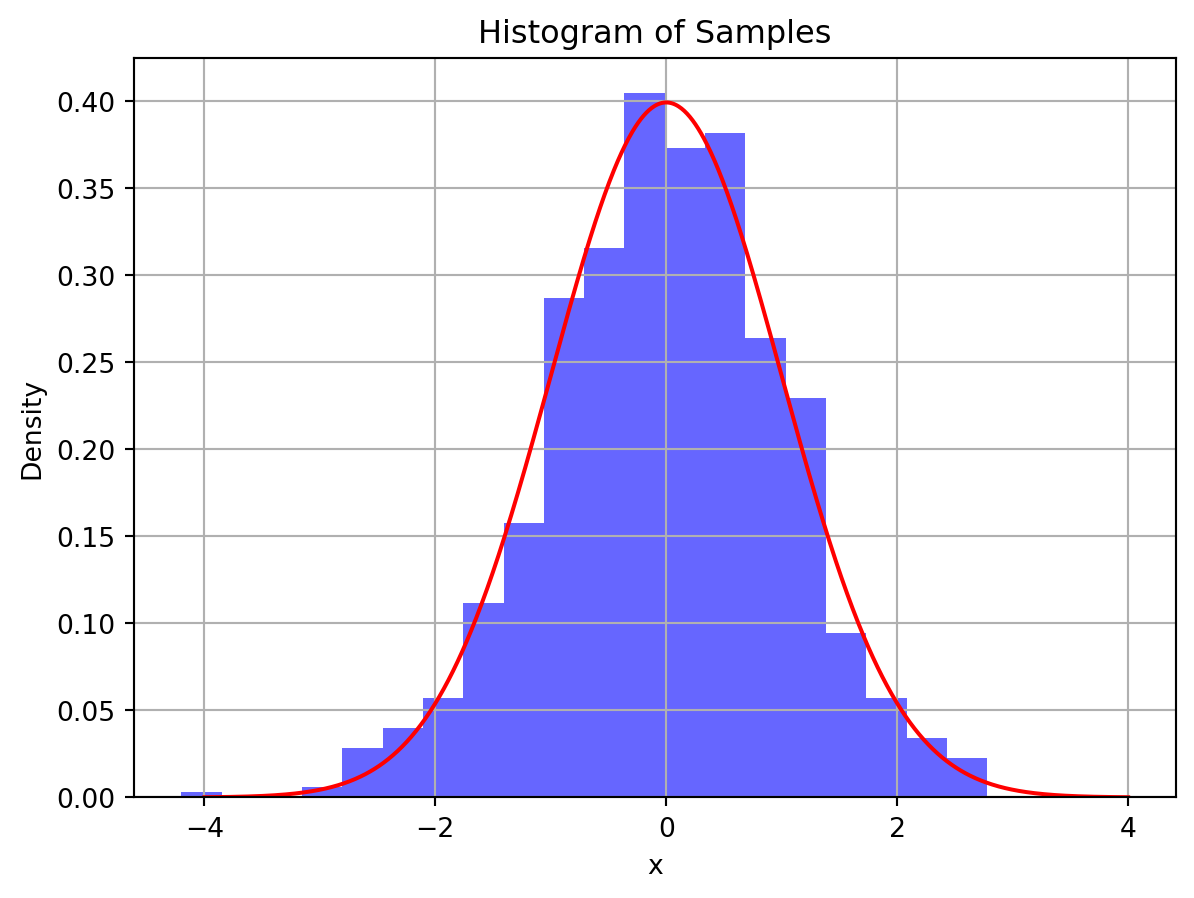

6.4 練習問題

Exercise 6.1 表が出ることを1、裏が出ることを0とする。\(X\) をコイン投げの結果を表す確率変数とすると、\(X\) は1または0の値を取り、表が出る確率は \(P(X=1)=0.5\)、裏が出る確率は \(P(X=0)=0.5\) である。確率変数 \(X\) の確率質量関数を scipy.stats モジュールを用いて定義し、表が出る確率 \(P(X=1)\) を計算せよ。

Exercise 6.2 標準正規分布に従う確率変数 \(X \sim N(0, 1)\) の累積分布関数を scipy.stats モジュールを用いて定義し、以下の確率を計算せよ。

  1. \(P(X \leq 0)\)
  2. \(P(X \leq 1.96)\)
  3. \(P(-1 \leq X \leq 1)\)

Exercise 6.3 正規分布に従う確率変数 \(Y \sim N(10, 2^2)\) の累積分布関数を scipy.stats モジュールを用いて定義し、以下の確率を計算せよ。

  1. \(P(Y \leq 8)\)
  2. \(P(Y \leq 12)\)
  3. \(P(8 \leq Y \leq 12)\)