複数の論理ゲートを組み合わせれば,より複雑な論理回路(logic circuit)を作ることができる.論理回路は,演算や記憶などを行う.
論理回路には,組み合わせ回路(combinational circuit)と順序回路(sequential circuit)の2種類がある.
組み合わせ回路¶
組み合わせ回路は,入力信号の状態に応じて出力信号が決まる.例えば,加算を行う加算器が該当する.
半加算器¶
コンピューターでは,もっとも基本的な演算は加算である.加算を行う論理回路は加算器(adder)と呼ばれる.加算機には,半加算器(half adder)と全加算器(full adder)がある.ここでは、半加算器について説明する.
半加算器は以下のような加算を行う.
半加算器は、二つの入力信号とを受け取り、二つの出力信号とを生成する.ここで、はSum(和)を表し、はCarry(桁上がり)を表す.
半加算器は、次のような真理値表で表される.
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
,,だけを見ると,これはXORゲートで実現できる.,,だけを見ると,これはANDゲートで実現できる.したがって、半加算器は次のように表現できる.
Figure 1:半加算器
順序回路¶
順序回路は,入力信号の状態と内部の状態に応じて出力信号が決まる.例えば,記憶ができるSRラッチやが該当する.
SRラッチ¶
SRラッチは、1 bitの情報を記憶するための基本的な順序回路である.
ここでは、二つのNORゲートを用いたSRラッチについて説明する.
NORゲートは、入力信号が両方とも0のときに出力が1になるゲートである.
| 出力 | ||
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
SRラッチは、(Set)と(Reset)の二つの入力信号を持ち、出力信号はとで表される.は記憶されている値を表し、はその否定を表す.
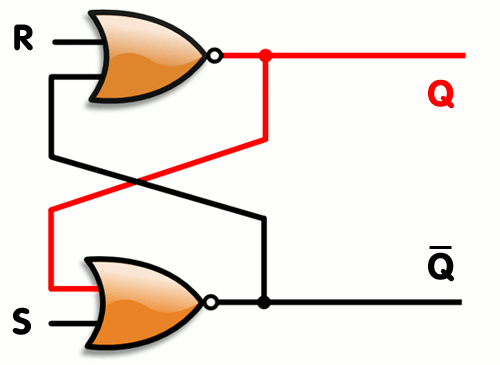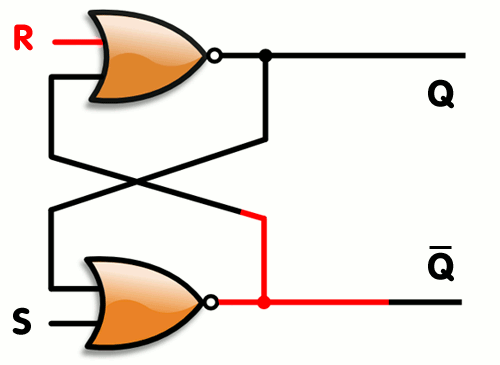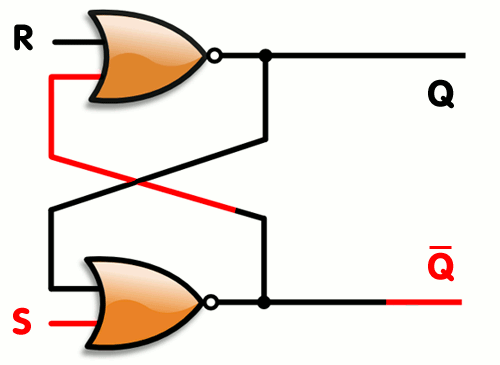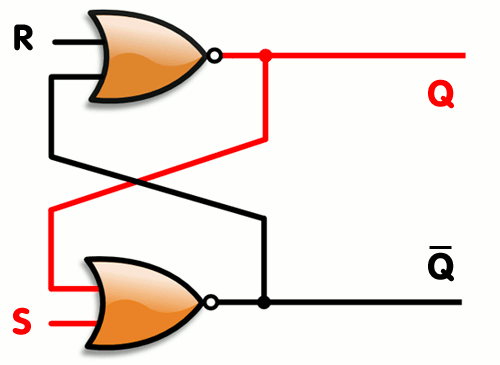
Figure 2:SRラッチ
SRラッチの動作は次の通りである.
,のとき、,となる.「セット」状態になる.
次に,のとき、出力は変化せず、,のままとなる.「保持」状態になる.
,のとき、,となる.「リセット」状態になる.
次に,のとき、出力は変化せず、,のままとなる.「保持」状態になる.
,のとき、出力は不定となる.
初期状態では、,とする.との初期値は不定である.
集積回路¶
集積回路(IC: Integrated Circuit)は、多数の論理ゲートを一つに集約したものである.集積回路は、論理ゲートの数に応じて、次のように分類される.
| 略語 | Full Name | Number of Gates |
|---|---|---|
| SSI | Small-Scale Integration | 1-10 gates |
| MSI | Medium-Scale Integration | 10-100 gates |
| LSI | Large-Scale Integration | 100-100,000 gates |
| VLSI | Very Large-Scale Integration | 100,000+ gates |
(N. Dale and J. Lewis, Computer science illuminated, 7th ed. Sudbury, MA: Jones and Bartlett, 2024.)
CPU¶
コンピューターにおいて、最も重要な集積回路は中央処理装置(CPU: Central Processing Unit)である.
練習問題¶
以下の図に示す論理回路の真理値表を作成せよ.
Figure 3:問題1
| A | B | Output |
|---|---|---|
| 0 | 0 | ア |
| 0 | 1 | イ |
| 1 | 0 | ウ |
| 1 | 1 | エ |
以下の図に示す論理回路の真理値表を作成せよ.
Figure 4:問題2
| A | B | Output |
|---|---|---|
| 0 | 0 | ア |
| 0 | 1 | イ |
| 1 | 0 | ウ |
| 1 | 1 | エ |
|